
 | |
|
Главная
>
Амплитудно и частотная характеристика АС Як( )>= 1, Tt(s)=И{s) = (cs+c,s)/(c,s+c,s>+CгS + CгSc ). В области низких частот T{s) система с пассивным излучателем с малыми потерями аналогична передаточной функции фильтра верхних частот типа Золотарева-Кауэра (см. гл. 3) четвертого порядка. Ачх системы с пассивным излучателем имеет провал иа самых низких частотах, тогда как АЧХ фазоннверсиой системы обладает монотонным характером (рис. 4.2,в). Закрытая система с корректирующим фильтром верхних частот первого порядка, включаемым перед уоилнтелем звуковой частоты, характеризуется передаточлой .функцией вида [4.3]: Г (.) = Яа,(5)Яи(!), Яи(5) = 5,/(?.+ 1), (4.4), (4.5) где Як1 (s) - передаточная функция фильтра верхних частот первого порядка; S = j( /o)i - комплексная частота, иормироваииаа относительно частоты среза фильтра ссц; Яд2(5) - передаточная функция закрытой системы [см. (4.2)]. В области низких частот Гз(5) закрытой системы с фильтром-корректором верхних частот первого порядка аналогична передаточной функции фильтра верхних частот третьего порядка с крутизной спада АЧХ 18 дБ/окт. (рис. 4.3,а). 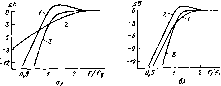 Рис 4.3 Пример амплитудно-частотных характеристик закрытых систем с корректирующими фильтрами верхних часгот первого (а) и второго (б) порядков: / - АЧХ системы без фнчьтра, 2 - АЧХ фильтра. 5-АЧХ системы с фильтром Закрытая система с дополнительным корректирующим фильтром верхних частот второго порядка характеризуется передаточной функцией вида Г,(5)=Яка5)Яд,(5), KK,(s) = sf/(d,-b<iiS.+d.). (4.6), (4.7) Wk2(s) - передаточная функция фильтра верхних частот второго порядка, Ядг - передаточная функция закрытой системы (см. В области низких частот Ti{s) закрытой системы с фильтром-корректором верхних частот второго порядка аналогична пере-1аточиой функции фильтра верхних частот четвертого порядка с футизиой спада АЧХ 24 дБ/окт. (рис. 4.3,6). Фазоийверсная система с малыми потерями с фильтром-коррек- тором первого порядка описывается в области низких частот передаточной функцией вида [4.4] T,(s)nls)H,{s). (4.8) Як ( ) - передаточная функция фильтра верхних частот первого порядка (4.5), Hn{s) - передаточная функция фазоинверсной системы (4.2). Передаточная функция фазоинверсной системы с малыми потерями с фильтром-корректором первого порядка в области низких частот аналогична передаточной функции фильтра верхних частот пятого порядка с крутизной спада АЧХ 30 дБ/окт. (рис. 4.4,а), 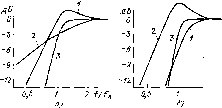 2 f/f. Рис, 4.4. Пример амплитудно-частотных характеристик фазоинверсных систем с корректирующими фильтрами верхних частот первого (а) и второго (б) порядков: 7-АЧХ системы без фильтра, 3 - ,АЧХ фяльтра, 3 - АЧХ системы с фильтром Фазоннверсная система с малыми потерями с фнльтром-коррек-тором второго порядка описывается в области низких частот передаточной функцией вида [4.4] Г.(5}=ЯК2(5)ЙА.(5), H2(s) -передаточная функция фильтра верхних частот второго порядка (4.7), Яа4(5) - передаточная функция фазоинверсной системы с малыми потерями (4.3), Ts{s) фазоинверсной системы с фильтром-корректором второго порядка аналогична передаточной функции фильтра верхних частот шестого порядка с крутизной спада АЧХ в сторону низких частот 36 дВ/окт. (рис, 4.4,6). Применение активного фильтра-корректора верхних частот на входе усилителя звуковой частоты позволяет, как будет показано ниже, существенно уменьшить амплитуду смещения подвижной системы в области низких частот н тем самым повысить допустимый уровень входной электрической мощности и максимального звукового давления. Передаточная функция закрытой АС с амплитудным корректором выглядит в общем виде аналогично (4.1): П(в)=Нк(з)Н,{8), (4.9) где Ядг(s)-передаточная функция закрытой системы (4.2) ~ передаточная функция амплитудного корректора. Функция Т (s) закрытой системы с амплитудным корректором, таким образом, представляет собой передаточную функцию фильтра верхних частот второго порядка, ио с более низкой граничной частотой (рис. 4.5): Передаточные функции систем с электромеханической обратной связью [4.1] и с электронным управлением механическими параметрами громкоговорителя за счет комплексного выходного сопротивления усилителя мощности [4,5] отличаются тем, что в выражении для Ha{s) эквивалентные параметры громкоговорителя также являются функцией параметров соответствующих электронных цепей. 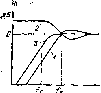 Рис, 4.5. Пример амплитудно-частотной характеристики закрытой системы с аи-шштудным корректором: - / - АЧХ системы без корректора, 2 - АЧХ кор- Цт ректора, 3 -АЧХ системы с корректором Иа приведенных выше выражений для передаточных функций систем различного тнпа можно определить АЧХ, ФЧХ и ГВЗ: АЧХ: 20 lg IT (s)J = 20 Ig {Re [Г (s)] + Im [Г ]} .. (4.11) ФЧХ: arg (Г (s)J =arc tg {Im [T (s)I/Re [T (s)]}, (4.12) rB3:-d{arg[T(s)]}/dm, (4.13> Re[7(s)] - реальная часть T(s), Im [Г (s) ]-мнимая часть T(s).. Обобщенная эквивалентная акустическая схема низкочастотного оформления АС. Коэффициент полезного действия, амплитудно-частотная характеристика Передаточная функция акустической системы в области нижних частот Ha{s), рассмотренная выше, определяется из обобщенной эквивалентной акустической схемы. Порядок ее построения методом электромеханических аналогий детально изложен во многих работах по электроакустике, например [2.3]. Общий вид эквивалентной акустической схемы показан яа рис. 4.6. В данной системе электро-мехаио-акустических аналогий напряжения а схеме .представляют собой звуковые давления, а токи - объемные скорости. Для анализа схемы и получения аналитического выражения для КПД, АчХ, ФЧХ и I. д. системы того или иного, типа необходимо
|