2.4. Движение в поле магнитного диполя. Метод Штёрмера

Общий случай движения заряженной частицы в поле диполя был рассмотрен Штёрмером. Здесь мы кратко рассмотрим его метод. Подробно метод изложен в монографии Штёрмера [2].

Если напряженность магнитного поля, создаваСхМого диполь-ным моментом а, равна В, а г, m и v соответственно заряд, масса и скорость частицы, то уравнение движения запишется в виде

=-vXB. (1)

Введем цилиндрическую систему координат (/?, ф, г) так, чтобы ось Z была параллельна диполю. В этой системе координат уравнение (1) принимает вид

dR dt

dq) \2

тс dt

dt 2

eR /

dq) 4t

Положим ds

dt dt

vdt и введем штёрмеровскую длину

(2) (3) (4)

где p = mv - импульс. Рассмотрим положительно заряженную частицу. Траектории отрицательно заряженных частиц являются зеркальным отражением траекторий положительно заряженных частиц относительно плоскости, проходящей через ось z.

При чисто математическом рассмотрении удобно выразить все длины в единицах с однако для физических приложений желательно, чтобы эта величина входила в формулы.

Если действуют только магнитные силы, следующие соотношения остаются справедливыми и для релятивистских частиц,

если под т подразумевать релятивистскую массу.

Уравнение (4) после подстановки формул (14) - в случае положительного заряда принимает вид

(16) разд. 1.2

d ds

d(p ds

3Rz dz ds

Зг2 dR -t(

где г==(г2--/2)

)2\l/2

После интегрирования получаем

jR R

c ds

где 2y - постоянная интегрирования, пропорциональная угловому моменту на бесконечности. Замечая, что

ds I

\ ds J

ИЗ (2), (3) и (6) получаем 1 dR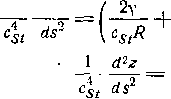

( dz \2

ds j \ ds

/ 2y

R \2

(7) (8) (9)

Полагая составляющую скорости Rdldt{= Rv djds) равной ysin, находим

d (cl,R 2ycsi

(10)

A поскольку I sin е-1 <1, то

R cl

<1.

Штёрмер показал, что значение у определяет характер орбиты. Если y>0, частица никогда не достигает диполя. При -КуО частица может, двигаясь из бесконечности, подойти к диполю. Одна из орбит при у = - 1-окружность радиуса r=cst, лежащая в экваториальной плоскости. Если у<-1, существуют две разрешенные области движения: внешняя {r>Cst), удаленная от диполя, и внутренняя (r<cs() вблизи него. В последнюю группу входят такие периодические (или квазипериодические) орбиты, которые можно рассматривать методом возмущений.

Рассмотрим простой случай - экваториальную плоскость (r = R). Частицы достигают экватора под углом , определяемым условием (10)

sin

(12)

Если задан импульс частицы, то тем самым определена величина Cst. Для Cst>R при заданном значении и у>-1 орбита начинается в бесконечности, а при у<-1 частица движется по периодической орбите (и никогда не покинет окрестностей Земли).

Граница между орбитами, начинающимися на бесконечности, и периодическими орбитами определяется условием у = - 1. Для

2.4. Движение в поле магнитного диполя. Метод Штёрмера 57 sin = 1

R = Cst. (13)

Согласно формуле (5), импульс в таком случае равен

а = = б.10<(-) -. (14)

где Re - радиус Земли. Частицы, имеющие больший импульс, могут приходить к экватору из любого направления. Для sin&== =-1 получаем

R{\+Y2) Csf

Соответствующий импульс равен

А = (3 - 2 /2-) 1,0 . 10- () . (15)

Частицы с меньшим импульсом вообще не могут достичь экватора. Если величина импульса р заключена в интервале рх<р< </?2, частицы подходят к экватору в пределах конуса с углом раствора определяемым формулой (12).

В разд. 2.5 будет показано, что задачу о движении заряженных частиц в космических магнитных полях часто можно в значительной мере упростить, если использовать метод возмущений.

Исключение составляют проблемы, связанные с космическими лучами, поскольку при высоких энергиях, характерных для космических лучей (10-10 эв), радиус кривизны нельзя считать малым по сравнению с радиусом Земли. В таком случае для расчета орбит следует пользоваться методом Штёрмера и в общем случае приходится прибегать к численному интегрированию. Труды Штёрмера, положившие начало данному направлению, подытожены в его книге [2]. Численные расчеты были сделаны Леметром, Валларта [16, 17] и другими [18-22]. Данному вопросу посвящены также опубликованные в последнее время обзоры [23, 24].

Знание траекторий космических лучей важно в нескольких отношениях. При изучении широтного эффекта, который позволяет определить спектр импульсов космических лучей, существенными являются расчеты той наименьшей энергии, при которой частица может достичь наблюдателя на определённой широте. Для интерпретации телескопических измерений космических лучей необходимо знать отклонение траекторий частиц в геомагнитном поле. Если телескоп, находящийся на некоторой широте, направлен в определенную точку неба, то возникает проблема расчета первоначального направления частиц, регистрируемых телескопом [25].