меняется в пространстве, означает, что существует ток, плотность которого дается уравнением Максвелла

rotH

а р-магнитная проницаемость жидкости. Ток создает объем-

ную силу, которая равна

1 \

rotHXB.

Поскольку в и Н имеют только компоненты вдоль оси г, выражение для F можно переписать в виде

grad

Это означает, что при наличии поперечного сжатия магнитное поле создает восстанавливающую силу, эквивалентную силе, возникающей при некотором распределении давления, численно равного В/8лр, - так называемое магнитное давление. Благодаря этому возможно существование волн сжатия - магнито-звуковых или магнитоакустических волн, которые могут распространяться поперек магнитного поля в результате комбинированного действия гидростатического и магнитного давлений.

Такие волны впервые были исследованы в работах [1-3 будут рассмотрены в разд. 3.8.

3.3 Основные уравнения

Чтобы сформулировать задачу математически, необходимо начать с уравнений Максвелла

rotH

rotE

1 дЪ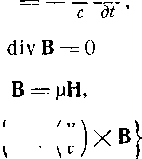

(3) (4)

где О - электрическая проводимость. К этим уравнениям нужно добавить гидродинамическое уравнение движения

pO + ({)xB-grad/p

и уравнение непрерывности

div (pv).

Здесь р - массовая плотность, р - давление, а G - силы неэлектромагнитного происхождения, действующие на единицу массы жидкости. В уравнении (6) мы опустили члены, связанные с силами вязкости (см. разд. 3.9). Для анализа поведения сжимаемой жидкости нам необходимо также соотношение между изменением давления и соответствующим изменением плотности. Для изотропной плазмы, в которой происходит обратимый адиабатический процесс, мы имеем

/7 = const р,

- отношениз удельных теплоемкостей. Приведенные соотношения доказываются в руководствах по термодинамике (см., например, [4]). В плазме, находящейся в магнитном поле и характеризуемой малой частотой столкновений, распределение скоростей может быть анизотропным, так что простое соотношение (8) оказывается неприменимым (см. [5]). Мы ограничимся рассмотрением только тех случаев, для которых справедливо уравнение (8).

3,3.1. Член, содержаиий магнитную силу

Член уравнения (6), содержащий магнитную силу, можно переписать при помощи известного векторного тождества

grad (ab) = (а grad) b -f (b grad) a + a X rot b -f b X rot a.

Используя также соотношение (1) и предполагая, что \х постоянно, а производная dlldt пренебрежимо мала, получим для объемной магнитной силы выражение

/ i \

X в = - grad + (В grad) В. (10)

Интерпретируем эту с:илу иначе. Если мь1 рассмотрим произ-вЪльный объем 1/, то результирующая сила получается интегри-

рованием по этому объему. Объемный интеграл можно затем преобразовать в интеграл по поверхности. Таким образом, результирующую силу можно представить как совокупность эквивалентных поверхностных сил, (Это возможно потому, что магнитная сила имеет природу дивергенции тензора, см., например, 6].) Для преобразования нам необходимы векторные тождества

grad = ф dS

(agrad)bflfl/= Г b(adS)- fbdivaal/,

(12)

где S - поверхность, ограничивающая объем V, dS - элемент поверхности, ф - произвольная скалярная функция, а а и b -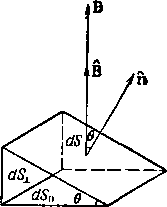

dSyrdScosB dS=dSstne

Рис. 3.4. К интерпретации эквивалентных поверхностных сил.

произвольные векторные поля. Применение этих тождеств к выражению (10) дает

В (В dS)

(13)

Введем единичные векторы: п, перпендикулярный к поверхности (и направленный наружу от объема V), и В, параллельный магнитному полю (рис. 3.4); получим dS = ntiS, B = BS и

Ъ dS = В dS (Вп) = 5 rf5 cos 9,

где 8 -у1:ол между магнитными силовыми линиями и .нормалью к элементу поверхности. Тогда уравнение (13) можно