Первый интеграл справа вычисляем непосредственно:

Так как f(z) непрерывна, то можно выбрать р настолько малым, что в круге внутри 7 \fiz) - / (Zq) \ < е, где е - сколь угодно малое положительное число. Для этого значения р

J z - Za \z - Za{ J p

r r T

так как путь интегрирования равен 2т:р. Это и доказывает формулу Коши (8).. Продифференцировав (8) раз, по.аучаем

1.3.8. Ряд Тейлора. Пусть /(2) - функция, голоморфная внутри круга С с центром в а\ Zq - точка внутри этого круга. По формуле Коши. имеем

Запишем

Тогда

-Za Z - а - (го - а) z - а z - а

z~z~ z-a г.-д-ТУТ--- \z-a) \ Z - а

так как \Zq - а<2: - а\. Умножим обе части этого выражения на

и проинтегрируем вдоль контура С. Это возможно, так как рассматриваемый, ряд сходится равномерно относительно точек окружности. Имеем

г-=/(2о; = Ло--Л1(2о - )+ ...-h (o- /-l- -. (10)

2 ,/ У (га)

Согласно формуле (9)

л.=: (.2,

Таким образом, получаем разложение в ряд Тейлора, распространенноа-на функции комплексной переменной: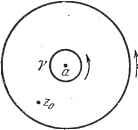

Рис. 1.23. криволинейных интеграла берутся в положи-

тельном направлении. Согласно соотношению (10) предыдущего пункта первый интеграл имеет вид

\] f -dz=A,-f-A,(z-a)+ ... -A {z-ar-t ....

где в си.ау формулы (11)

А --l- f /() dz

Равенство (12) в данном случае использовать нельзя, так как /(г) голоморфна не во всех точках внутри Г.

При а = 0 (центр круга в начале координат) получим

/(о) = /(0)+4/(0)+ ... +/( (0)+ ...

Это ряд Маклорена.

1.3.9. Особые точки. Точка, в окрестности которой аналитическая функция разложима в ряд Тейлора, называется обыкновенной точкой. Всякая необыкновенная точка называется особой точкой.

Полюса - это изолированные особые точки, вблизи которых /(г)

остается однозначной и которые являются обыкновенными точками для yj

Существенно особые точки - это изолированные особые точки, в окрестности которых /(г) остается однозначной, но которые являются особыми

И для функции yj-

Критические точки или точки разветвления - это особые точки, вблизи которых функция f{z) не остается однозначной.

Примеры особых точек. Функция имеет полюс 2-го порядка в начале координат.

Функция 21Г1 имеет простые полюса z = -\-J и z - -J (ср. стр. 49).

Функция sin у имеет существенно особую точку в начале координат.

Функция е имеет в точке z = а существенно особую точку. Функция г/ имеет точку разветвления в начале координат.

1.3.10. Разложение в ряд Лорана. Дана функция f{z), имеющая полюс или существенно особую точку z-a. Если выделить эту точку-маленькой

окружностью Y радиуса р, то функция /(г) становится голоморфной внутри круговой области, заключенной между 7 и окружностью Г с радиусом R, также имеющей центром а (рис. 1.23). Применим форму.ау Коши к контуру 7-[-Г. Обозначив через Zq-точку внутри кругового кольца, получаем

A-n = -ff(z)(z-ar-dz. (13)

Таким образом, получаем разложение в ряд Лорана

+ Ло+Л,(го-а)-- ... -\-A (zo-а) -\- ...

Коэффициенты Л и Л определяются формулами (11) и (13).

Так как р можно выбрать сколь угодно малым, то точка Zq может быть сколь угодно близка к точке а. Следовательно, разложение в ряд Лорана представляет собой разложение в ряд функции f(z) вблизи полюса или существенно особой точки. Использование разложения в ряд Лорана позволяет более точно классифицировать полюсы и существенно особые точки.

Если в ряде Лорана имеется только конечное число коэффициентов типа А , то особая точка является полюсом для рассматриваемой функции.

Обозначим через наивысшую степень . входящую в разложение Лорана. Число п есть порядок по.аюса; если ге = 1, то полюс называется простым.

Если разложение Лорана содержит бесконечное число членов с отрицательными степенями z - а, то точка а является существенно особой точкой.

Примеры. Дана функция

z(z-l)-

Найдем ее разложение в ряд Лорана вблизи полюса г- = 0. Имеем

1 1 (1+2+22-1- ...) = -4 - 1-г-г- ...

- z(z-l) - V I - . - . г

Вблизи полюса z - 1 имеем

111 1

z{z-\) z-\ \-\-{г - \)~ z-\

J--1 +(2-1) -(2-1)2-1- ...

Рассмотрим, далее, функцию е>. Найдем ее разложение в ряд Лорана вблизи существенно особой точки 2 = 0. Непосредственно получаем

е - i г + 2! 2 + 3! п\ z

Второй интеграл вычисляем аналогично первому. Имеем

1 1 J 1

Zo - z Zo - a - (2 - a) Zo - a j z - a

2o - a

Так как \Zq-a\>\z--a], то полученное выражение можно разложить в ряд и проинтегрировать:

JL fMaz=:--+- ... +7--V +

2nj J zo - z Zo - a> (zo - a)