dt ~ дх-

Произведем замену переменных, положив и = х-\- at, v = х - at. Тогда нетрудно показать, что это уравнение принимает вид

dz ди dv

Отсюда

2 = ф( ) + ср(г;) и, возвращаясь к прежним переменным,

z = .x + at) + (x~at). рассмотрим частный случай, полагая

ф (X + аО = Л sin k(x-h at), ср (х - at) - Л sin й (X -- at).

Соответствующее рещение будет

z - 2Л cos kat sin kx.

Покажем, как можно применить полученное рещение к задачам из теории электричества.

Рассмотрим полностью изолированный линейный проводник, омическим сопротивлением которого будем пренебрегать (рис. 6.1). Положение произвольной точки М этого проводника определяем криволинейной абсциссой 5. Пусть 5 - криволинейная абсцисса точки В.

Обозначим через i и v соответственно силу тока и потенциал в точке М в Момент времени t. Если переместиться по проводнику на единицу длины, то падение напряжения будет вызвано самоиндукцией рассматриваемого участка. Отсюда получаем

Рис. 6.1. -Wir-

Точно так же изменение силы тока на единицу длины будет вызвано тем, что часть тока будет щунтирована емкостью рассматриваемого участка. Отсюда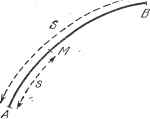

) Можно было бы получить этот результат, применяя соображения предыдущего пункта, но здесь проще прямое вычисление.

а затем иначе говоря

2; = ф(х) + ср(у).

Здесь ср и (j) обозначают две произвольные функции. Обратимся теперь к уравнению колебаний струны

dz , dz

= У f (s) sin п-к-ds.

т. е. являются коэффициентами Фурье для функции f (s).

6.3.4. Телеграфное уравнение. Это уравнение вида

=CL + iLG + CR) + GRE.

Око решается применением операционного исчисления (см. гл. VIII, п. 8.4.10 и последующие).

6.3.5. Уравнение Лапласа. Это уравнение вида

-53 + + = 0 ==0. (31)

в задачах о распространении волн часто встречается уравнение вида

dW , дЮ , дЮ I дЮ 1 дЮ

или Ш -

дх ~~ с dt ~ с dt

В этом случае, разлагая искомую функцию в ряд по синусоидальным функциям времени, члены которого имеют вид

U{x, у, Z, t) = eU{x, у, Z),

мы придем для функции U (х, у, z) к уравнению Гельмгольиа

S + + ДtУ-/г2tУ=0. (32)

Дифференцируя уравнения (29) И (30) соответственно по и s и исключив функцию V, получим

. J J :

dt ~ LC ds

Будем считать, что для любого момента времени t сила тока i - i{s. t) равна нулю на концах проводника:

г(0. t) = i{S. t)=0,

а при, = О

i(S, O)f(s).

где /(5) - известная функция, удовлетворяющая условиям

/(0) = /(S)-=0.

Легко видеть, что решение поставленной задачи может быть удовлетворено суперпозицией полученных выше частных решений волнового уравнения, т. е.

i(s, t)= у, а COS--т-sin п-!: -.

Действительно, граничные условия удовлетворяются, так как / - О при 5 = 0 и i- = 5. При = О получаем

Решение удовлетворяет начальному условию, если коэффициенты а выШ-сляются по формуле

Стоящая перед инженером задача заключается не в отыскании общего решения уравнения (31) или (32). Ему нужно найти такое конкретное решение, которое удовлетворяет на некоторых поверхностях определенным граничным условиям. В качестве -граничных условий могут быть заданы значения функции (задача Дирихле) или ее производной по некоторому направлению (задача Неймана). Эти значения могут быть либо известными постоянными, либо, чаще всего, известными функциями координат.

Решение задачи существенно упрощается, если рассматривать ее в системе ортогональных криволинейных координат, для которой заданные поверхности входят в семейство (или в несколько семейств) координатных поверхностей.

Пусть р, ср, Ь - координаты выбранной системы. Естественно частный интеграл уравнения (31) или (32) искать в виде

f/(p. ср. &) = /?(р)Ф(ср)в(&),

в котором каждая из функций R, Ф, 0 зависит только от одной координаты р, (р, &. Этот частный интеграл будем называть произведением Лапласа.

Функции R, Ф, © содержат произвольные постоянные. Линейный характер уравнений (31) и (32) показывает, что эти уравнения удовлетворяются некоторой конечной или бесконечной, дискретной или непрерывной суммой произведений Лапласа, в которых произвольные постоянные принимают все возможные значения. Кроме того, в этой сумме каждое произведение Лапласа может сопровождаться првизвольным коэффициентом. Искомым решением будет такая сумма произведений Лапласа, в которой произвольные коэффициенты принимают значения, обеспечивающие выполнение граничных усповий.

Таким образом, решение уравнений (31) и (32) сводится к Следующей задаче: найти произведения Лапласа в рассматриваемой ортогональной системе криволинейных координат. Выражения для произведений Лапласа, полученные в следующих пунктах, позволяют также найти решение некоторых часто встречающихся дифференциальных уравнений, например дифференциального уравнения для функции U Бромвича (формула (87) п. 6.3ЛЗ).

Известно (п. 3.4.2), что в системе ортогональных криволинейных координат, где квадрат элемента длины равен

ds = el dx\ -Н el dx -\- el dxl.

лапласиан Ш имеет вид

23 ди

dxi \ е, дх

11 дх2\ дх2 ) дхз

eie2 dU\

, ез дхз)]

Здесь е обозначают локальные единицы длины. В такой системе

уравнения (31) и (32) имеют вид:

д I €263 ди\ . д (6361 ди

dxj \ е, дх,

(6263 ди

dxi \ 1 дх

дХ2 \ 62 дХ2

езв, ди \ , д

6162 ди

дхз \ вз дхз

6,02 Ш\

(33)

2 дх2, дхз \ вз дхз,

В рассматриваемых ниже различных системах координат мы будем искать произведения Лапласа, удовлетворяющие уравнению (34). Из них, полагая ft - О, мы получим произведения Лапласа, удовлетворяющие уравнению (33). Для некоторых менее употребительных систем координат мы ограничимся рассмотрением одного только уравнения (33).