3. Система параболических координат вращения (параболои-дальные координаты) (см. п. 3.4.6):

x - cap cos ф, у = cap sin ф, z=]c (Р - а).

Ш ==

с2(а2--р2) L да

д и дЧ7

1 ди

1 ди

дЧ/

С а

)Р2 а

= Л, COS --2 sin (Аф,

A:B,J(pa)-\-B2Y(poi), B==CJ{p)-\-C,K{p).

4 Система тороидальных координат (см. п. 3.4.1 Dish i sin ф sh £ cos ф sina

=-0,

sh S cos ф

ch £ cos Ш ch S + cos ? ch £ -j- cos у

(ch ; + cos ш)-*

rd U

1 d U

do sh i d\> J , ch e -j- cos Ш

l-j-cosfflch£ df/ , . dU

d? .

= 0.

б= ]/cli t-+cos Ф 2

= i-4;os -Ь Aj sin Ф = B, cos vcp + 2 sin ф,

Е-=С,Я , (chf) + C2Q i(chS).

5. Система бисферических координат (см. п. 3.4.11):

sh£

, (ch £ -}- cos у)

sin ш sin i]v sin Ш cos ij

ch 5 + cos <p ch £ 4- cos ч>

ch £ 4- cos <p

1 df/

d£2

do sm 9 di ch £ + cos Ш

1 -f cos у ch £ dU je dU

sin <p dy d£ .

= 0.

и = Vch?4-coscp 2 *Ф, 4 = Лi cos лф-Ь 2 sin р.ф,

Ф = i (cos ф) + S2Q 1 (COS ф).

-г 2

Ё = С, ch 4- sh

Замечание. Функции, входящие в приведенные выше произведения Лапласа, написаны в наиболее общем виде. Совершенно ясно, что условие существования функции U в определенной области приводит к ограничению общего набора функций, составляющих произведение Лапласа. Это было показано на примерах в предыдущих пунктах. В частности, нередко р. и v являются целыми числами, и тогда следует отбросить функции Y, К, Q.

Следует также заметить, что определения функций и различны в зависимости от того, заключается ли их аргумент между -1 и -1,

находится ли он вне этого интервала или, что бывает чаще всего, является комплексным числом (см. приложение к п. 7.6.25).

6.3.12. Уравнение Пуассона. Это дифференциальное уравнение вида

Д£/ = /(х, у, Z). Оно совпадает с формулой Пуассона (см. п. 3.3.10)

если предположить, что электрлческие ааряды распределены с Плотностью - е/(х, у, z). Поэтому рещение уравнения Пуассона естественно искать в виде скалярного потенциала непрерывной системы электрических зарядов, Докажем, что действительно выражение

t-i = - / dl, r{x~-x,f + iy-~yrf + iz-z,f (*)

дает частное рещение уравнения Пуассона. Здесь х, у, z - текущие координаты точки, Ху, уу, Zi - координаты точки наблюдения, а di - элемент

объема области i.

Согласно формуле Грина (см. п. 3.3.8)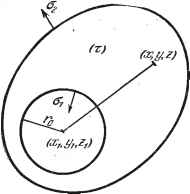

С (Г

(66)

л(1)=о.

поскольку

Поверхность с состоит из внутренней стороны поверхности Cj, ограничивающей сферическую полость с центром (Xj, уу, Zy), и внещней стороны поверхности ограничивающей область т (рис. 6.2),

Будем предполагать, что U вместе со своими частными производными ограничена внутри т и на а. Устремим к нулю радиус сферической полости.

тогда /М

Рис. 6.2.

aCTi тоже стремится к нулю, а пределом второго интеграла

по поверхности Cj: j f/grad rfoj будет 4тс/(Xp у i) *). Пусть теперь и - рещение уравнения Пуассона, т. е. U.U = /(х, у, z). В силу (66) получаем

/ di + 4.U(x у z,)f

grad и

/ 1 М и grad da-

Правая часть этого выражения представляет собой вклад в функцию U интеграла по внещней поверхности области т. Отметим, что эта часть, с точ-

*) Напомним, что dci направлена внутрь сферической полости.

rot =8

div£==0, .

divH = 0.

Запишем эти уравнения в ортогональной системе координат, квадрат элемента длины в которой равен

ds = ej dx] -j- dx\ -j- dxi.

*) Строгий вывод см. в [8], стр. 171-175. **) См. там же.

ностью до множителя дает решение уравнения Лапласа

Af/(xi. zO = 0.

которому соответствует / = 0.

Предположим, что в любой конечной области функция U к ее частные производные ограничены и при стремлении г к бесконечности U имеет порядок г~, а ее производные - г~. Будем называть такие функции U правильными. Для правильной функции выражение в квадратных скобках имеет порядок (при больших г), и при /->оо интеграл справа стремится

к нулю. Следовательно, выражение

.4 1 г f(x,y,z}dxdydz

где интеграл распространен на все пространство, представляет собой решение уравнения Пуассона.

Полагая в этой формуле / = 0 вне области т, убедимся*), что 11, из (*) является частным решением уравнения Пуассона внутри т. Обозначим через U общее решение уравнения Пуассона и положим U - U,=:W. Тогда AW = 0. т. е. W - общее решение уравнения Лапласа.

Итак, общий интеграл уравнения Пуассона дается формулой

где и, - частный интеграл уравнения Пуассона (*), а W - общий интеграл уравнения Лапласа.

Отметим, что правильное решение уравнения Пуассона во всем пространстве единственно, оно дается формулой (**). Это следует из теоремы Лиувилля: гармоническая во всем пространстве функция, исчезающая на бесконечности, тождественно равна нулю **).

Замечание. Уравнение Пуассона играет основную роль не только в электростатике. Оно, наряду с уравнениями динамики, описывает законы электронной оптики.

6.3.13. Решение уравнений Максвелла методом Бромвича. Если выразить электрическое и магнитное поле в рационализированной системе МКСА, то уравнения Максвелла для среды с диэлектрической постоянной е и магнитной проницаемостью р. получают вид:

rot £ = - р