fix) 1! ,

J IL ,

x x x

- 3!

L t-4~dt

--x--h- -

! / t-e-*dt= ....

2! 3! t-r-n -i ( -)

Рассмотрим ряд. частная сумма которого равна

1 1! , 2! , (-!) -( -1)!

В данном случае = 0. Имеем

оэ со

так как оба интеграла, входящие в эти соотнощения, положительны. Значит,

\finix)\=\x>{f{x)-S {x)]\<-.

Если X бесконечно возрастает, то R (x) при фиксированном п стремится к нулю. Следовательно, 5 (х) представляет собой частную сумму асимптотического разложения /(х). Соответствующий ряд расходится при любому, так как нарущается необходимый признак сходимости.

Используем этот расходящийся ряд для вычисления /(Ю). Тогда общий

член разложения равен оп+Г убывает по абсолютной величине от

/1=1 до =10, а затем растет до бесконечности. По доказанному выше.

/(х)-5 (х)-<

Поэтому за приближенное значение /(10) выгодно принять Siq. Тогда соответствующая ошибка будет меньше

= 0,0000362 ...

Повторным интегрированием по частям найдем

Следующая таблица и рис. 7.1 показывают последовательное убывание и возрастание частных сумм рассматриваемого асимптотического разложения:

Если в определенной области изменения z функция допускает асимптотическое разложение, то это разложение определяется единственным образом.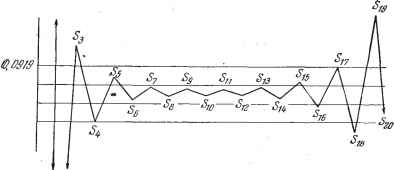

SfOfiS

Рис. 7.1.

Действительно, полагая в условии существования асимптотического разложения последовательно я=1, 2.....получаем

йо= lim /(г), й]= lim

UI- oo z->oo

2= lim zAf{z)~a - \, ...

Напротив, две различные функции могут иметь одно и то же асимптотическое разложение. Классический пример представляют собой две функции, отличающиеся на при RCp) Действительно, коэффициенты асимптотического разложения при г > О, вычисленные с помощью полученных выше формул, тождественно равны нулю.

Пусть существуют асимптотические разложения функций /(г) и g{zy.

Тогда справедливы следующие теоремы:

Произведение (г) называется главным членом асимптотического представления /(г).

7.1. ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ

Гиперболические функции играют важную роль при расчете длинных линий.

7.1.1. Определения. Положим (ср. формулы, выражающие круговые -функции через ei-, п. 1.1.10)

ch X = {е -4- е~-*) (гиперболический косинус х), shx = -(e - е~) (гиперболический синус х),

gjj qX Q - X

th x = = x g-x (гиперболический тангенс x) .

Полагая k=cosx, C = sinx, имеем i?-\-(,=\. Точно так же, полагая ? = chx, C==shx, имеем -Точка с координатами С расположена на окружности в случае круговых функций и на равносторонней гиперболе в случае гиперболических функций.

1. Общий член асимптотического разложения a.f(z)-\-g(z) равен

2: Общий член асимптотического разложения произведения функций Jiz)g{z) равен

3 а м е ч а-н и е. Если ф О, то можно делить на асимптотическое раз--ложени.е giz).

3. Если функция разложима в степенной ряд, сходящийся при 1/1 < Р то асимптотическое разложение функции

Т(г) = ф(/(.))

получается непосредственной подстановкой в степенной ряд фС/) асимптотического разложения /(г) (при условии йд<р).

4. Если /(г) и fiz) допускают асимптотические разложения, то асимптотическое разложение /(г) получается почленным дифференцированием асимптотического разложения /(г).

5. Если /(г)-Jj ! <го=<1 -0). то асимптотическое разло-

-жение J f{z)dz получается почленным интегрированием асимптотического

разложения /(г).

Замечание. Иногда функция /(г) не имеет асимптотического разложения, однако существует такая функция g{z), что отношение допускает асимптотическое разложение. Тогда можно написать

fiz)g{z)Uo + + -+ ..