Еще более глубокая аналогия существует между круговыми и гиперболическими линиями. Рассмотрим окружность -\-= \ (рис. 7.2) и гиперболу Р - с2=1 (рис. 7.3). Пусть 714-точки на этих кривых, Р - основания ординат М, Т - точки пересечения ординаты А с лучом ОМ, М-точки,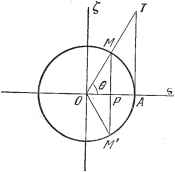

Рис. 7.2.

Рис. 7.3.

симметричные точкам М относительно оси абсцисс Примем за независимую переменную криволинейную площадь ОМАМ и обозначим ее о. Вычислим длины отрезков AT, ОР и РМ как функции о.

Уравнение гиперболы в полярных координатах: р2 cos 26=1. Отсюда

1 Г d2b 1 , , о\

Используя эту зависимость между о и 6 и уравнение гиперболы р =(cos 26) получим (см. рис. 7.3)

лг=tge =

= th о.

ОР = р cos 6 =

ch о.

РЖ =: OP tg 6 = sh о.

Для окружности 0 = 6, и потому непосредственно получаем аналогичный результат:

ЛГ = tgo, OP = coso, PM = sino.

Используя определения гиперболических функций, нетрудно вывести следующие формулы:

cos X = ch ух, ch X = cos ух; ysinx = shyx, yshx = sinyx; ytgx = thyx, ythx = tgyx; J sh (й ± г ) = sh Й ch & ± ch Й sh b, \ ch{a + b) = ch Й ch & ± sh Й sh b;

{sh 2й = 2 sh Й ch a, ch 2u = ch2Й + sh2Й = 1 4-2sh2c = 2ch2a-1;

chx=l-f-2--- ... sh x = x-l--gy-j- ...

(2/г)! +

x + (2n-f 1)!

И, значит,

91-92=arctg ;;i y2

Рассмотрим кривую, определяемую уравнением

Легко заметить, что это - окружность с центром на оси Ох. Кривая, определяемая уравнением

= -g-arctg х~у ( я часть 8),

- тоже окружность, но с центром на оси Оу.

Гиперболические функции имеют период 2t:j, совпадающий с периодом функции е:

sh (х Н- 2ЫJ) = sh X, ch (X + 2kTzу) = ch х.

7.1.2. Обратные гиперболические функции. Пусть x = shK, тогда через Arshx обозначают аргумент гиперболического синуса, т. е. функцию

и = Arsh X = In (х + /х2+Т)-

Таким же образом формуле х = ch м соответствует

M = Archx = ln(x ± ]/ х2- I)

и формуле X = th м

M = Arthx==ln /

Функции Arshx, Archx, Arthx читаются соответственно: ареасинус. ареако-синус, ареатангенс.

7.1.3. Приложение гиперболических функций к расчету длинных линий. Метод Броуна. Абаки Блонделя - Кеннеди. Изучение распространения электрических сигналов вдоль линий передач часто приводит к необходимости вычисления выражений вида

а ch 7 + р sh 7,

где комплексные числа а, р, -у зависят от характеристик линии.

Разработан графический способ расчета этих выражений (метод Броуна).

Положим - = thS. Тогда

achT4-NhT=Sil-

Очевидно, что

8 = Arth-==:cH-y&.

Выразим вещественную и мнимую части Ь(а и Ь) через х и у, представляющие собой вещественную и мнимую часть 2= - . Используя формулы пп. 7.1.2 и 1.1.11, получим

S= Arth2 = ln= [ln 11 1+ у (9, -<Р2- 2ft)].

Так как г==:х--уу, то

ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ

Пусть окружность первой системы, соответствующая параметру а, пересекается с окружностью второй системы, соответствующей параметру Ь,

В точке с аффиксом . Тогда веще-ственная часть Arth ~ равна а, так как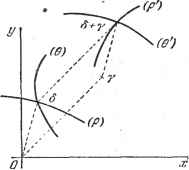

Рис. 7.4.

Рис. 7.5.

точка находится на первой окружности, а мнимая часть Arth - равна , так

как точка находится и на второй окружности. Следовательно, для определения чисел fl и & достаточно найти окружности рассмотренных семейств,

пересекающихся в точке с аффиксом - (рйс. 7.4).

После вычисления § нужно определить ch8 и ch (8-{-(). Обратимся к вычислению ch 6. Модуль р и аргумент 6 величины ch 6, где 8 х -f- /у,

соответственно равны

W 9 6 7 6 5 3 2 1 О

p==]Ach2x - sin2y, tge = thxtgy.

Каждое из этих выражений определяет семейство кривых в плоскости ху.

Рассмотрим две кривые, принадле-. жащие к двум разным семействам и пересекающиеся в точке с аффиксом 8. Значения параметров р и 6 для каждой из этих кривых дают соответственно модуль И аргумент ch8. Имея точку с аффиксом 8, можно по правилу параллелограмма

4 -3 -2 -7 О 1 Рис. 7.6.

2 3 i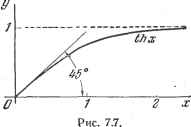

непосредственно построить точку с аффиксом 8-]-Т затем найти модуль и аргумент р и 6 для величины ch(8-)i[-) (рис. 7.5). В большинстве случаев на одной плоскости изображают обе системы окружностей рис. 7.4 и оба семейства кривых рис. 7.5. Эти графики называются абаками Блонделя - Кеннеди.

7.1.4. Графики функций sh х, chx, tbx (рис. 7.6 и 7.7).