Пример. Найти вычет -относительно z - a. 1-й способ.

т. е. Res(a)=e (l +- .

2-й способ. Переместим начало координат в точку а, положив z = u-\-а:

Вычет равен коэффициенту при т. е. е 1+-- . Следовательно,

-j- f j~~dz = е для любого контура С, окружающего точ-

ку z = a.

1.3.14. Лемма Жордана. Часто бывает полезно рассматривать открытые контуры интегрирования, точнее, контуры, которые в действительности замыкаются бесконечной окружностью комплексной плоскости. В большинстве случаев речь идет о прямолинейном контуре, замыкающемся полуокружностью с центром в начале координат, радиус которой растет до бесконечности. Если интеграл по этой полуокружности стремится к нулю, то контур интегрирования сводится к бесконечной прямой. Следующее положение, известное как лемма Жордана, позволяет указать важный частный случай равенства нулю интеграла по полуокружности бесконечного радиуса.

Пусть Ф(г) - функция, голоморфная в верхней полуплоскости (О < arg Z < тс), за исключением конечного числа полюсов., и стремящаяся к нулю при 2;->оо равномерно относительно argz. Тогда при >0

lim Г е гф (2) = О,

где контур С представляет собой полуокружность с центром О и радиусом R, замыкающую верхнюю полуплоскость.

Действительно, произведем замену переменной

z = ReJ\

Очевидно,

jg/</?cose-<;?sine j g-</?sine

В силу .равномерного стремления Ф (z) к нулю, для достаточно больших R

имеет место неравенство Ф (z) ] < е, где е - положительное, произвольно

sine, 2 п

малое. Используя, далее, неравенство---, справедливое при Oargz

<; Y, получаем

It It/2

У Ф(z)edz <sR f е-пб < 2s/? /* e-2Wde = !(1 < , ,

с 6 6

что и доказывает лемму.

Если t отрицательно, то в условии леммы следует только заменить верхнюю полуплоскость на нижнюю (- ii: < arg г < 0) и соответственно верхнюю полуокружность на нижнюю.

Рассмотрим теперь

Этот предел равен нулю при тех же условиях, что и предыдущий, если для t положительного и отрицательного речь идет соответственно о левой

полуплоскости Y < arg z < и о правой полуплоскости - < < ]

относительно мнимой оси. Контур С обозначает соответственно полуокружность с центром О и радиусом R справа или слева от мнимой оси.

Замечание. При вычислении интеграла по бесконечной оси с помощью теоремы о вычетах следует помнить, что контур, образованный осью и бесконечной полуокружностью, должен обходиться в положительном направлении.

1.3.15. Применение леммы Жордана к единичной функции. Рассмотрим функцию вещественной переменной t, определенную с помощью интеграла в комплексной плоскости:

(14)

Контур С представляет собой ось х с выемкой в форме полуокружности со стороны отрицательных у (рис. 1.25).

Обозначим через 7 часть контура С, ограниченную двумя точками А и В, равноотстоящими от начала координат, и через Г полуокружность с центром О, проходящую через А и В и находящуюся под действительной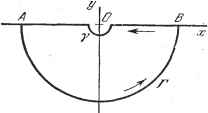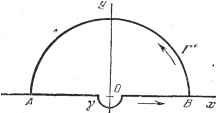

Рис. 1.25.

Рис. 1.26.

осью. Контур 7 +Г не содержит особых точек подынтегральной функции. Следовательно, соответствующий криволинейный интеграл равен нулю.

Если предположить, что t отрицательно, то по лемме Жордана интеграл по контуру Г стремится к нулю, когда радиус окружности бесконечно возрастает. Следовательно, предел интеграла по контуру 7 (т. е. интеграл по контуру С) равен нулю:

1 Г о

Положим теперь, что t положительно. Рассмотрим полуокружность Г, проходящую через А и В и расположенную со стороны положительных у (рис. 1.26). В этом случае

2яу ./ ш

так как вычет относительно точки О равен единице. По лемме Жордана интеграл по контуру Г стремится к нулю, если радиус окружности бесконечно растет. В пределе имеем

(1ш=1 при > 0.

Рис. 1.27.

Функция fit), определенная равенством (14), равна нулю при / < О и единице при >0 (рис. 1.27). Она представляет собой единичную функцию или единичный импульс и обозначается через ri{t).

Приведем другое выражение для 7j(). Повторяя предыдущее рассуждение, получим

2ic/ ./ ю I

Следовательно, мы можем написать

[ О для t>0.

1 1

2 2-!tj

sin №t

<1ш

для t < о, для > 0.

Так как

sin сй

является четной функцией, не имеющей особенности при

ш = 0, то справедливо равенство

sin <j>t

(15)

1.3.16. Интегрирование при наличии точки разветвления. Рассмотрим простой пример и проиллюстрируем на нем, какие следует принять предосторожности при интегрировании по контуру, внутри которого имеются точки

разветвления. А именно вычислим интеграл zdz. Контур С - окруж-

ность с центром А и радиусом R.

Если точка z перемещается по этой окружности, то можно положить z - ReJ. Рассмотрим точку г= Re<>. В этой точке функция имеет два значения:

Yz,=

Возьмем первое значение этого корня, а саму точку Zq в качестве отправной. Имеем

с , e;

Величина интеграла зависит не только от значения, выбранного для zk, но также от отправной точки интегрирования и радиуса окружности.

Таким образом, при вычислении интеграла по контуру, внутри которого находятся точки разветвления функции, требуется предварительно фиксировать определенную ветвь функции и отправную точку интегрирования.