2Y b

т + 2

Уравнение (90) относится к типу (91) при ;re = 0, с = 0. Положим в (91) параметр а равным нулю. Уравнение

у [Ьх + ]У=

имеет общее решение

т+2 \ л \2

(93)

Если, кроме того, мы приравняем т = 0 и напишем параметр с в виде - /(/+О- то уравнение (91) принимает вид

у + [ь-]уо.

Оно имеет общее решение

y = / xZ i{xY~b).

Если в уравнении (91) приравнять а==0. с = 0, то мы получим уравнение

у + Ьху = О, общее решение которого имеет вид

у=/х2 (2х). (94)

Если, кроме того, т = 1, то находим общий интеграл уравнения

у + Ьху = 0,

который равен

Если в уравнении (91) параметр с положить равным нулю, то получим У + -У + Ьху = 0. (95)

Это уравнение имеет общее решение

y = (96)

т + 2

Часто встречающееся дифференциальное уравнение

dy\

x-\+bx у = 0

dx \ dx j

е что иное, как уравнение (95), в котором т = - а и а -а.

Всюду в предыдущем предполагается, что ;re + 2-.±0. В частности, общие решения -(92)-(94), (96) не годятся, если ;re+2 = 0. Если предположить .т~ - 2, то уравнение (91) получает вид

xy +axy+ky = Q.

имеет общее решение

Это уравнение Эйлера (п. 6.2.9). Оно сводится, если положить х = е, к линейному дифференциальному уравнению с постоянными коэффициентами

Уравнение

при b ф имеет общее решение

у =e-Z[{b - ayx Если b = а, то легко заметить, что

У1 = хе-а- , у2 = х-е~ -

представляют собой при уфО два линейно независимых решения. Если v =:0. оба эти интеграла превращаются в один, но легко проверить, что тогда выражение е - 1п х будет решением. В этом случае получаем общий интеграл в виде

y=e- M-f Bin X).

Ниже указывается несколько видов дифференциальных уравнений, приводящих к особенно простым решениям. Они не входят в типы уравнений, приведенных выше.

Уравнение

у + [~-2g (X)] y + \l- + [g(x)F -g(x) - } у = 0

допускает в качестве общего решения

y=J XU)-Отметим также следующие два частных случая предыдущего уравнения;

/ + (i - 2 tg л.) у + JEi) у = О, у = Z.(x);

y + (i+2dg.)/-(-), = 0, > = ад Пример. Найдем общий интеграл

у -b-y-lQxy==0.

Сопоставление с уравнением (91) дает

а = 5. с = 0, г) = -16, 1 = 4. Отсюда, подставляя эти значения в (92), получаем искомый общий интеграл

y = x-Z2(jJxy

Некоторые примеры применения бесселевых функций

7.5.37. Колебание однородной тяжелой нити, подвешенной за один конец. В качестве первого применения бесселевых функций естественно привести именно этот пример, так как впервые бесселева функция была найдена Даниелем Бернулли в 1732 г. при изучении колебаний однородной

тяжелой нити. Разумеется, современное название и подробное описание обширное семейство бесселевых функций получило лишь много времени спустя, ибо только в 1824 г. Бессель, исследуя вопросы, связанные с возмущением движения планет, детально изучил свойства этих функций.

Итак, дана гибкая тяжелая нить длиной I единиц, подвешенная за конец А (рис. 7.27). В состоянии покоя она свободно висит вдоль вертикали АО. На практике модель совершенно гибкой нити можно осуществить, пользуясь цепью с достаточно мелкими звеньями. Выведем нить из положения равновесия, сместив конец ее В налево и попробуем найти закон, описывающий перемещения нити, ограничиваясь небольшими плоскими колебаниями. Примем АО за ось Ох, а прямую, которую конец В очертит при малом смещении, за ось Оу.

Пусть р - масса нити на единицу длины, а М, М--две бесконечно близкие точки. В каждой точке нити действует натяжение Т, обусловленное весом, горизонтальная составляющая которого будет

г- С)

Горизонтальная составляющая силы, действующей на элемент длины нити ММ, будет равна приращению величины (*) при переходе от Ж к М. На единицу длины нити эта сила будет равна

J - dxVdxj-На высоте х приближенно имеем T~\>.gx, отсюда ду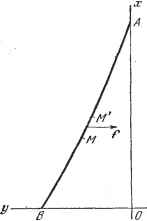

Рис. 7.27.

ду , ду

Сила инерции на единицу длины равна p-g- Уравнение движения по горизонтали будет

g dt дх дх

Ограничимся синусоидальными функциями времени вида у = ср (х) е- . Тогда

rfcf <i>

- = 0.

dx X dx g X

Чтобы вычислить общий интеграл этого уравнения, достаточно положить 2x = z2 или же, проще, сравнить его с уравнением (91). Решение (92) получает в этом частном случае вид

<р(х) = лл(2а,/ ) + БКо(2а,-/).

Так как решение должно иметь конечное значение для х = 0, то

При х = 1 (в точке подвеса) имеем у = 0. Следовательно, величина

2w\/ ---корень функции Jia.). Пусть будет одним из корней уравне-

ния Уд(а)=;0. Имеем