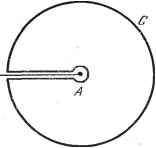Разрез

Рис. 1.28.

На практике вычисление производится следующим образом. Точку разветвления А соединяют с контуром С дугой, не имеющей двойных точек, которую Z при движении вдоль С не может пересечь. Таким образом осуществляется разрез. Точка z может перемещаться по замкнутому контуру Г,

состоящему из контура С, малой окружности, заключающей точку разветвления, и обоих берегов бесконечно узкого разреза (эти берега обходятся в противоположных направлениях). Отметим, что контур, состоящий из обоих берегов разреза и малой окружности, иногда называют шнуром (рис. 1.28).

Наличие разреза обязывает функцию /(z) снова принимать прежнее значение, когда Z возвращается в исходную точку, какой бы при этом ни был описан путь внутри Г или на нем. Действительно, при таком- движении аргумент точки z может изменяться только на величину, меньшую Внутри контура Г функция /(z) становится голоморфной (кроме как в конечном числе полюсов), и поэтому можно применить теорему о вычетах. Интеграл, взятый по контуру С, начиная от заданной начальной точки (искомый интеграл), сложенный с интегралами по разрезу и по малой окружности, будет равен сумме вычетов относительно полюсов, находящихся внутри Г.

Следует заметить, что существует глубокое различие между разрезом, описанным в п. 1.3.12 (замечание 1) и рассмотренным в данном пункте. В последнем случае интегралы по различным берегам разреза не компенсируют друг друга, так как значения, которые принимает функция /(z) в двух бесконечно близких точках на разных берегах разреза, существенно отличаются друг от друга. Рассмотрим, например, функцию z . Если бы не было разреза, то любую точку /?, можно было бы представить как точку/?, 6q-]-2tc,-для этого требуется лишь осуществить один поворот около точки разветвления (в положительном направлении). И тогда функция l/z

вместо начального значения ? е приняла бы значе-

ние ?е2 ei. На верхнем и нижнем берегах разреза в точках окружности С функция z принимает соответственно значения у/?/ и -у/?/.

1.3.17. Контур Бромвича. Контур Бромвича представляет собой прямую, соединяющую точку с - у сю с точкой е-- усю, оставляющую слева от себя все осо- c-Jco

бые точки рассматриваемой функции (рис. 1.29). Величина с, равная расстоянию от контура до оси у, всегда Рис. 1.29. положительна.

В задачах, относящихся к движению устойчивых механизмов или дисси-пативным электрическим цепям, особенности функций в большинстве случаев находятся либо слева от мнимой оси, либо на ней самой. В первом случае мнимую ось можно считать контуром Бромвича. В задачах о распространении электрических или акустических волн некоторые из особых точек являются точками разветвления, в других задачах - это, как правило, полюса.

1.3.18. Интеграл Бромвича - Вагнера. Бромвич и Вагнер определили форму интеграла, встречающегося при решении технических задач с помощью операционного исчисления (см. теоремуФурье - Меллина, п. 8.3.22). Этот интеграл имеет следующий вид:

C+JCO

где Ф(2:) - функция, все особенности которой лежат слева от контура Бромвича.

1.3.19. Эквивалентный контур. Если функция Ф(г) удовлетворяет условиям леммы Жордана, то интеграл по бесконечной полуокружности, расположенной слева от мнимой оси, равен нулю при > 0.

Рассмотрим типичные эквивалентные контуры для особых точек разного

типа.

1. Все особенности являются полюсами. В этом случае контур, эквивалентный контуру Бромвича, состоит из произвольной замкнутой кривой, не имеющей двойных точек, внутри которой расположены все полюса. Значение интеграла по контуру Бромвича равно сумме вычетов относительно этих полюсов.

2. Функция имеет точки разветвления. В качестве контура, эквивалентного контуру Бромвича, можно взять малую окружность, заключающую точку разветвления, соединенную разрезом с бесконечной полуокружностью, лежащей слева от мнимой оси.

Примеры эквивалентных контуров.

эквивалентный контуру Бромвича, - окружность с динат (рис. 1.30).

Для функции р- контур, центром в начале коор-

Для функции

контур, эквивалент-

ный контуру окружности с

Бромвича, центром в

состоит из малой начале координат,

с-1-Jco

c-jcx)

c+Joo

c-Joo

Рис. 1.30.

Рис. 1.31.

являющемся точкой разветвления, соединенной с бесконечным полукругом, как это показано на рис. 1.31.

Для функции , имеющей две точки разветвления в z= ±.J,

У 2 -I- 1 .

можно начертить множество эквивалентных контуров. Несколько таких контуров показано на рис. 1.32.

Пример 1. Вычислить

C+jco

ydz ( > 0, целое).

2-KJ J z +

C-jca

Особенность Ф (z) представляет собой кратный полюс в начале координат. Так как условия Жордана выполняются, то интеграл будет равен вычету функции относительно точки г = 0.

Cd-JOO

C-Joo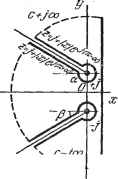

C¥-JCO

C-i-Joo -

Рис. 1.32.

c-Joo

Разложим e в ряд. Вычет относительно особой точки z = О равен коэффициенту при - в произведении

1+Z/4-

Т. е.

I и!

c+jco

пример 2. Вычислить / = 2 f

с-JCO

2(1- е-йг)

. Условия Жордана

выполнены. Особенностям!} функции являются, во-первых, двойной полюс в начале координат, во-вторых, бесконечное число простых полюсов

Z ==---п, когда п принимает все целые значения от -сю до -(-оо, кроме

значения г = 0. Следовательно, интеграл / равен сумме вычетов относительно полюсов подынтегральной функции.

Вычислим вычет относительно точки г = 0. Для этого разложим в ряд числитель и знаменатель подынтегральной функции:

1 + + +-

fe2 1

...)

2! 3!

При малых z это выражение можно записать в виде

z4 , , hz . hz

(,+.+ +...)(>+4+igi+...)

Вычет равен коэффициенту при -, т. е. --(-i.