Так как корней бесчисленное множество, последнее равенство определяет бесконечное количество видов возможных нормальных колебаний нити.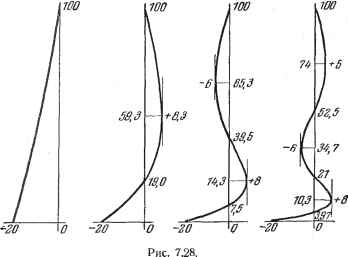

На рис. 7.28 изображены несколько первых видов этих колебаний. Смещения нарисованы с большим увеличением для того, чтобы с большей наглядностью показать формы, принимаемые нитью.

7.5.38. Исследование решения волнового уравнения в цилиндрических координатах. Рассмотрим произвольное поле, которое распространяется вдоль некоторого направления. Примем это направление за ось z. Поле характеризуется скалярной функцией времени и координат F{x, у, z, t). Обычно при изучении явлений распространения функция F определяется как решение волнового уравнения

1 д Р

LF-.

Здесь с обозначает скорость распространения. Если ограничиться рассмотрением синусоидальных функций времени, то, как мы видели в п. 6.3.7, в цилиндрических координатах, которые часто оказываются естественно приспособленными к такого рода задачам, общий интеграл представляет собой сумму всех частных произведений Лапласа вида

Мы уже видели, что если радиального ограничения не существует, иначе говоря, если (f может свободно возрастать на углы, большие чем 2ic, то v является целым числом. При этом говорят, что для функции F имеет место симметрия повторения порядка v вокруг Oz. Если ось Oz является частью области существования функции, то коэффициент В должен быть равен нулю, так как из физических соображений функция F не может принимать бесконечные значения.

Если q - вещественное число, функция F представляет собой величину, периодически изменяющуюся вдоль оси Oz. Если же q - комплексное число

И экспоненциально затухает

а-ур, функция F имеет псевдопериод вдоль Oz.

7,5.39. Колебания равномерно натянутой мембраны. Рассмотрим мембрану, т. е. упругую тонкую пластинку, равномерно натянутую на плоскую раму. Исследуем свободные колебания этой мембраны, выведенной из положения равновесия, исходя из следующих упрощений:

1) затухание не происходит;

2) смещения достаточно малы, чтобы можно было считать натяжение неизменным, а перемещения каждой точки соверщающимися по малым прямым, перпен дикулярным плоскости, которую представляет собой мембрана в покое.

Теория поверхностного напряжения указывает, что каждая единица поверхности мембраны подвергается воздействию нормальной силы, равной

где А - поверхностное натяжение, а и - главные радиусы кривизны *).

За ось Z примем ось, перпендикулярную к плоской поверхности мембраны в состоянии покоя и к двум прямоугольным осям Ох и Оу на этой плоскости. Пусть р - поверхностная плотность мембраны. Уравнение движения будет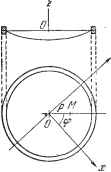

Если деформации малы, то, пренебрегая квадратами малых величин, имеем

1 , 1

дг dz

/?2 ~ дх ~ ду -

Рис. 7.29.

Если положить :

Колебание мембраны определяется волновым уравнением

А dt -

7.5.40. Случай круглой мембраны. Примем за ось z нормаль к поверхности круга в центре О (рис. 7.29).

: ft2, то уравнение движения в цилиндрических координа-

тах будет

}dz , L д

p f df

Ha рис. 7.29 указаны мембрана, закрепляющая ее рамка (кольцо) и координаты р и ср точки М мембраны. Если ограничиться только синусоидальными функциями времени, то частное решение примет вид

Z (р, ср, t) - е cos (ft(op),

так как смещение центра О конечно. Общим решением будет сумма всех частных решений, в которых п принимает все возможные значения.

*) Формула (*) совпадает с известным выражением для силы поверхностного натяжения жидкостей - выводится аналогичными рассуждениями. Разумеется, между А и коэффициентом поверхностного натяжения вещества мембраны а нет ничего общего. Величина А зависит от упругих констант, от толщины мембраны и т. д.

Узловые линии представляют собой геометрическое место точек мембраны, для которых смещения постоянно равны нулю. Различают два сорта узловых линий:

1) диаметральные узловые линии, которые выражаются уравнением cos 9= О,-это диаметры, разделяющие окружность на 2п секторов с углами при

вершине, равными (рис. 7.30);

2) круговые узловые линии, представляющие собой концентрические окружности, радиус которых определяется соотношением y (iup)=:0.

Круговая рамка радиуса R обязательно должна быть одной из таких узловых линий. Будем считать, что она соответствует р-му корню уравнения У (а) = 0,

иначе говоря, положим kmR = а.. Это выражение определяет частоту колебаний: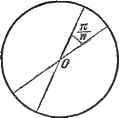

Рис. 7.30.

Имеется, следовательно, р - 1 }гзловых окружностей, соответствующих кор-

ням а а,

2 -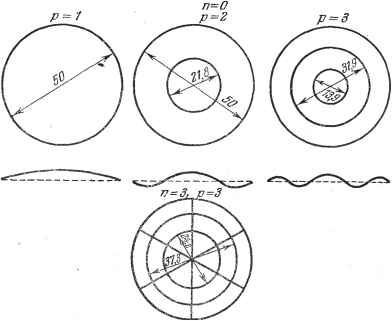

Рис. 7.31.

Если число п отлично от н}гля, то центр О представляет собой узловую точку, так как У(0) = 0. Это совершенно очевидно - ведь некоторое количество узловых диаметров обязательно пересечется в этой точке. Если же /г = 0, то узловых диаметров не существует, и мы имеем дело с симметрией вращения. Центр мембраны представляет собой пучность, так как Уо(0)= 1.