Замечание. В группы формул, написанных для поперечных магнитных и электрических волн, неявно входит постоянный коэффициент, зависящий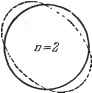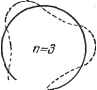

Рис. 7.33.

от выбора чисел т, п, 1. Он зависит от других граничных требований, относящихся к условиям возбуждения колебаний в полости (см. замечание 2 к п. 6.3.14).

Рассмотрим случай наличия у цилиндра радиальных перегородок. Допустим, что в цилиндре имеются две радиальные перегородки, образующие между собой угол па. К уже написанным выше условиям равенства нулю тангенциальных составляющих электрического поля на границе цилиндра следует добавить аналогичные условия, касающиеся обеих перегородок:

При cf = 0 и 9 = 2ir - та.

и fp, и добавить

Нужно исключить COS vcp из формул, выражающих к соотношениям, определяющим параметры, вместо условия \ - п новое соотношение

sin V (2тг - та) = О

(.9 - целое число).

2 -а

i i i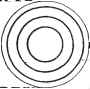

Рис. 7.34.

Число V, следовательно, теперь может отличаться от целого числа.

В частности, в случае, когда а=0, а) б)

т. е. когда перегородки сливаются

в одну, V = -g-. При четном s мы

снова приходим к уже полученным решениям, но при нечетном s имеет место ряд других решений, в которые входят J\, Уз. Уб. -

Т Т 2

7.5.42. Распространение электромагнитной волны внутри бесконечного кругового цилиндра. Вычисление здесь подобно вычислению, проведенному в предыдущем пункте. Так как речь идет о распространении вдоль оси Oz, то произведение Лапласа будет

sin f-P) -Граничные условия сводятся к требованиям

£ = £ = 0 при р = /?.

Параметр а определяется из уравнений У (ар) = 0 для поперечной магнитной волны, и У(ар) = 0 для поперечной электрической волны. Отсюда получаем следующие выражения для составляющих электромагнитного поля.

Поперечная магнитная волна (волна £):

л? / к; \ sin . .. ,

.=4i-p)cos -

Поперечная электрическая волна (волна Н):

£.=0.

Каждый тип волны определяется группой из двух целых чисел (с, п). Опре-деленной частоте f~- соответствует ряд возможных значений q;

1- ИЛИ

Если дан волновод с определенным радиусом R, волна самой низкой частоты, способная распространяться внутри цилиндра, будет соответствовать q - 0. Для волн Е она, кроме того, соответствует наименьшему не равному нулю корню Х. Мы знаем, что эта наименьшая частота связана с первым корнем Jx), равным 2,40483. Отсюда в пустоте для Е имеем

72145 /ш1п = Мгц.

Для волн Н наименьший не равный нулю корень соответствует первому корню ji{x) = 0, т. е. 1,8412. Отсюда в пустоте для Ну получим

55 236 /rain=~2 Мгц.

Естественно, что наименьшие частоты, соответствующие q - O, имеют бесконечную длину волны и бесконечную скорость распространения фазы в волноводе.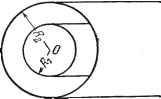

Можно спросить, почему решение а = О не принимается за первый корень Jn(x) (пфО) или / (х) (я. > 1).Если а -О, то мы вынуждены принять за функцию /?(р) в произведении Лапласа выражение

Af~\-Bp- .

Напишем Е, которая должна быть равна нулю при р = /? и при р = 0 (волна Е):

= - т {Арп- + Вр-п-Ц

Отсюда А = -В и и == 0. Это решение не подходит, так как оно приводит, с точностью до постоянного множителя, к выражению

E=:~e-i eJ \

которое бесконечно на оси Oz. В действительности нельзя приравнять Е к нулю, так как случай п = 0 был с самого начала исключен. Решение не годится также для волн Н.

7.6.43. Случай коаксиального проводника. Этим названием обозначают промежуток между двумя бесконечными цилиндрами, имеющими общую ось (рис. 7.35). Посмотрим, какие изменения следует внести в предыдущие вычисления. Функцию Y больше исключать не нужно, поэтому произведение Лапласа будет теперь иметь вид

/?(р) = ЛУ (ар) + ВК (ар).

Коэффициенты А а В определяются граничными условиями, которые следует записать в виде

AJAaR{) + BY,iaR0 = O,

AJ, (aR) + ВК (aR) = 0. Р -

Эта однородная и линейная система будет иметь ненулевое решение, если определитель ее будет равен нулю:

Jn ( i) Уп iaR) ~ J (aR) У iaR{) = 0.

Если через \ обозначить один из корней этого уравнения, то мы получим для поперечных магнитных волн

R (р) = Уп ihRi) Jn ih?) - Jn ihir) Уп ihp)-

Это же относится и к поперечным электрическим волнам, но здесь граничные условия приводят к выражению

(Р) К iV-fl) Jn М - Jn ((.l) п М

где через [х обозначены корни уравнения

Jn ( 0 к (2) - Jn (2) Уп iRi) = О-

Пользуясь формулами (88) и (89) п. 6.3.13, можно легко написать составляющие электромагнитного поля.

Если повторить рассуждения предыдущего пункта для наименьших не равных нулю корней и а,-, то может показаться, что здесь также имеется наименьшая частота для заданного проводника (предельная частота).