(1-2ft + /?2) 2(1-/г) = S .

n = 0

получаем тождество

п=0 п=0

из которого сразу следует Р (1)=1.

Заменим в (ПО) z на -z. Это можно сделать двумя способами:

[1 - 2й(-2)4-/?2]-= = [l - 2(-й)гН-/г2]~Ч

Приравнивая соответств}тощие правые части разложений, получим

PA-z)=i-irPniz). (121)

Отсюда, в частности,

Р (-!) = (-!) .

Положим в (ПО) Z - 0, затем разложим левую часть в ряд и приравняем коэффициенты при одинаковых степенях й. В результате получим

/2р+,(0)-0, Р,Д0) = (-1)-ц?2. (122)

7.6.11. Корни полиномов Лежандра. В п. 6.2.11 мы показали, что корни решений дифференциального линейного уравнения просты. Следовательно, корни Полиномов Лежандра просты. Функция g(z)~(z-1) имеет п корней, равных -f-l, и п корней, равных -1. Функция g(z), очевидно, имеет п-1 корней, равных +-1, п-1 корней, равных -1, и, как следует из теоремы Ролля, один корень между -1 и -f-l. Продолжая это рассуждение, получим, что полином ге-й степени g * >(2) имеет п корней, заключенных между -1 и --1, и, естественно, ни одного корня, равного -1 или --1. В силу формулы Родрига (117), это - корни Р (2;) = 0. Следовательно, все корни Pn(z) простые и находятся между -1 и -fl.

7.6.12. Интеграл Шлефли. Пусть z - аффикс точки комплексной плоскости переменной t. Рассмотрим интеграл, взятый по контуру С (рис. 7.42):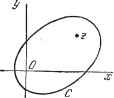

- fdt. (123)

Рис. 7.42. Если м = й - целое положительное число или нуль,

то этот интеграл представляет собой полином Лежандра Pniz). Действительно, интеграл (123) равен вычету кратного полюса порядка п-\- \ при t - z, т. е. (п. 1.3.13)

1 1

2 и!

который, в свою очередь, согласно формуле (117), равен Piz). Интеграл (123) называется интегралом Шлефли.

7.6.10. Некоторые значения полиномов Лежандра. Как указано в п. 7.6.3, полином (105) равен единице при z-l. Это легко проверяется с помощью формулы (ПО). Положим в (ПО) z-l. Учитывая, что

1 со

CUz)==2pCf:t\ {zy.

Полиномы Гегенбауера представляют собой решение дифференциального уравнения

и удовлетворяют соотношениям ортогональности

J (z2-1/ 2C(2)C(z)dz = 0 {тфпу -1

Замечание. При p~Q полиномы Гегенбауера CjJ определяются разложением в степенной ряд функции

1п (1 ~ 2hz Н- ft2) 2 {zy

л = 0

7.6.14. Функции Лежандра первого рода. По определению, функция Лежандра первого рода P(z) представляет собой решение дифференциального уравнения (99), принимающее при z=l значение 1.

Если в уравнении (99) произвести замену переменной С,= -

оно принимает вид

C(l-C).5 + (l-2C)4fH-v(v+l)/ = 0. (124)

Это частный случай дифференциального уравнения, определяющего гипергеометрическую функцию Гаусса (см. пример из п. 6.2.10), при а= -v.

Придадим постоянной значение 1, тогда

p;(z)=F[-v, v+i. 1; .

7.6.13. Обобщение полиномов Лежандра. Полиномы Гегенбауера.

Мы установили, что полиномы Лежандра могут рассматриваться как коэффициенты при различных степенях h в степенном ряде функции

(l 2ftzH-ft2) 2 gi<:l).

Полином Гегенбауера и-й степени с индексом р определяется как коэффициент при /г в степенном ряде функции

со л = 0

Случай р = /2, очевидно, соответствует полиномам Лежандра:

C](z) = PAz).

Способом, аналогичным способу установления рекуррентных формул для солиномов Лежандра, получаем соотношения

2zCr\z)-2C Uz} = C yiz}.

или, в виде ряда, , ,

РЛ)=1 + -+ - + > - + () . (125)

Если V равно целому положительному числу п или целому отрицательному числу -п-1, то ряд обрывается на члене, содержащем (1-г) . Располагая этот полином по степеням z, мы опять получаем полином Лежандра Р (z), определяемый формулой (105).

Если P{z) - решение (99), то Р(-z) также будет его решением. Предположим, что P{z) и Р(-z) линейно независимы. В этом случае общий интеграл (99) будет

fiz) = APAz) + BPA-z).

Рассмотрим вопрос о линейной независимости Р,(-z) и P.{z). Для этого изучим поведение P{z), когда z стремится к -1, или, при замене переменной 2 = cos.e, поведение P(cose), когда 6 стремится к -к. При этой замене переменной уравнение (99) приобретает вид

Если ограничиться рассмотрением значений 6, очень близких к нулю, то общее решение уравнения (126) будет очень близким к общему решению уравнения

равному

Это решение бесконечно возрастает, если 6 приближается к нулю. Так как при 60 функция P(cos6) стремится к --1, то Р(г) и Р(-z) линейно независимы только в случае, если Р(-z) бесконечно возрастает при z-l. Согласно (125), это имеет место при v нецелых, и, как нетрудно убедиться, порядок возрастания P.,(z) при z-1 тот же, что и у функции

lni± = i-lncos. . (127)

Так как обе функции P(cose) и 1 ( Ч-1)) принимают одинаковое значение --1 при 6 = 0, то Jo{G YI)) можно рассматривать как апрок-симацию P(cose) при малых значениях 6.

Если V равно целому числу п, то дело обстоит иначе. Действительно, в силу формулы (121),

и общее решение уже не будет равно

AP (z) + BP (-z),

так как P {z) не возрастает бесконечно, если z стремится к -1, а принимает значение (-1) . Следует ввести другое решение Q {z), линейно независимое от P (z). При этом общее решение будет

AP (z) + BQ (z).

Это решение Q (z), называемое функцией Лежандра второго рода, определяется в конце п. 7.6.19.