7.6.18. Определение функции Лежандра первого рода через интеграл Коши. Рассмотрим интеграл Шлефли (123). Подставив его в дифференциальное уравнение Лежандра, получим после несложных преобразований *)

2 ./ dt\ (t-zr at-i).

Если V - целое положительное число, то полученное равенство удовлетворяется. Это подтверждает то, что уже нам известно: интеграл Шлефли представляет собой решение дифференциального уравнения Лежандра. Функция

4V+1

(138)

если v - целое положительное, при полном обходе контура С принимает первоначальное значение. В этом Рис. 7.45. случае интеграл Шлефли, как показано в п. 7.6.12,

совпадает с полиномом Лежандра P (z). Пусть v -не целое число. Тогда интеграл Шлефли позволяет дать другое определение функции Лежандра первого рода.

Рассмотрим функцию (138). Она имеет три особые точки (точки разветвления): t=l, t - -1, t - z. Предположим, что контур С окружает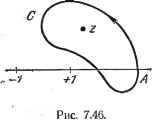

Рис. 7.47.

только точку =1. Если, исходя из точки А (рис. 7.45), обойти этот контур в положительном направлении, то новое значение функции ча в точке А равно первоначальному, умноженному на

g27c7(v+l)

Если же контур С окружает только точку t~z (рис. 7.46), то при обходе этого контура в положительном направлении функция in приобретает множитель

Значит, если контур С окружает две особые точки t= \ ш t - z (рис. 7.47), то при полном обходе контура функция w принимает первоначальное значение.

Следовательно, функция

V + 1

*) Ср. [1], п. 141.

представляет собой решение дифференциального уравнения Лежандра, котороесовпадает с полиномом Лежандра, если число v - целое положительное. При произвольном v эта функция определяет функцию Лежандра первого рода P,iz).

Чтобы добиться однозначности такого определения сферической функции, принимают, что в исходной точке А (точке пересечения контура С с осью абсцисс при >.1) равны нулю аргументы +1 и i-1, абсолютное значение аргумента t - z меньше тг и в плоскости t осуществлен разрез от точки = -1 до точки t=: - со (рис. 7.47).

7.6.19. Функция Лежандра второго рода. Определения. Используем вычисления п. 6.2.11. Решением (99), линейно независимым от P (z), будет

Pn(z)f (1 22){Я (2)р

Поэтому общее решение (99) для целых и положительных п имеет вид

Полином Лежандра P (z) имеет только простые вещественные корни а(г=1, п), лежащие внутри интервала (-1, 1). Поэтому можно

написать

1 Г 1

1 л

2 L 1-2 \~\-г

~ z - aj. (2 -

Коэффициенты вычисляются по формулам

г - rf2 L(1-2){P ()PJ.=

dz L(l-22){i(2)}4,=

Отсюда

P {z) = {z - a;)L{z).

Подставим (139) в уравнение (99) и положим затем z - a. Тогда (l-aZ.4a,)-a,L(a,)=0.

(139)

Следовательно, и можно написать

f{z)AP{z)+BP,{z)

1 , 1-f 2

Zsl Z- г

. (140)

Функция Лежандра второго рода, в соответствии с формулой (140), определяется следующим образом: для вещественных z, заключенных внутри интервала (-1, --1)- по формуле

Q ()-=n()

1 , 1 + 2

2- г

(141)

для комплексных z, а также для вещественных z, находящихся вне интервала (-1, +1), по формуле

2 г-1 jLi z - aj ]

r=I /

(142)

При таком определении функция Лежандра второго рода Q (z) вещественна при вещественных значениях z.

Функция Лежандра второго рода имеет две точки разветвления z = - 1 и Z = -)- 1. Соединяя разрезом точки z = - I и z = -\-l, выделяем однозначную ветвь этой функции.

Если последовательно придавать и значения О, 1, 2.....то, согласно

формуле (141), находим

Общая формула имеет вид

Q (z) = i P (z) In 4 -W , (z).

(143)

n(n-l)

1 n(n - l)

2(2n -1) J n(n-l)(n -2)(n -3)

- . . . } (144)

3 2(2n-1) 2-4(2n -l)(2n -3) n

Переход к формуле (142) при любом фиксированном п осуществляется

заменой в (143)- In на 1п .

Рассмотрим ряд (104), определяющий решение (99) для всех значений z, удовлетворяющих условию \z\y> 1. Легко убедиться, что функция, заданная рядом (104), при v = re, где п - целое положительное число, совпадает с функцией Q (z) с точностью до постоянного коэффициента

1.3-5... (2п - 1)