2V+1

в - эйлерова функция первого рода, определенная в п. 7.4.6.

Пусть V - целое положительное число и - l<z<4-l. Тогда можно показать, что функция Лежандра второго рода (141) совпадает с функцией, определенной тем рядом (101) или (102), который не вырождается в полином Лежандра, если положить

2-4...(п-1)

a-i-1) 2 - g -j-i- (n - нечетное число),

, -5- 2 4 ... и a - i-1) -J-g-(n - l) ( - четное число).

Аналогично тому, как это было сделано для бесселевых функций, можно определить функцию Лежандра второго рода с помощью пределов:

N 1- (г) cos 71/ - -г) 0 (Z) .-= lim ---:---- ,

-/TCV

/Г . , ,. ЯЛг)-- -ЯЛ-2) Q {z)~ hm -:-5-

Используя ряд (104) и повторяя рассуждения п. 7.6.17, можно показать, что функция (z) подчиняется тем же рекуррентным соотношениям, что и P(z). Следовательно, эти соотношения справедливы для любого интеграла (99). С помощью указанных выше формул определения нетрудно установить, что, функции Q принимают следующие значения:

Q2P (+ 1) = Q2P+1 (+ 1) = + cxd;

Q2p(-l) - oo. Q2pi( l) = -j-co; - .

lim Q (2)==0.

2-oo

7.6.20. Определение функции Лежандра второго рода через интеграл Коши. Мы видели в п. 7.6.18, что дифференциальное уравнение Лежандра (99) допускает в качестве решения криволинейный интеграл от функции

1 jt - 1)

взятый по такому контуру (комплексной плоскости t), что при его обходе функция (138) остается однозначной. Можно определить контур, отличный от контура, приведенного на рис. 7.45, который обладал бы тем же свойством. Мы видели, что при полном обходе в положительном направлении вокруг точки разветвления t = -\-l функция (138) умножается на е- Ясно, что при обходе точки разветвления t = - 1 в отрицательном направлении та же функция (138) умножается на е-Зи/( +!) Следовательно, если в качестве контура Г взять любую кривую, имеющую форму восьмерки

Ряд (104) можно взять в качестве определения функции Q(z) при произвольном V, полагая множитель равным

(t-iy

dt (145)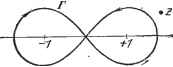

будет удовлетворять дифференциальному уравнению Лежандра. Это позволит определить функцию Лежандра второго рода Q(2) для любых значений индекса V и (за счет выбора допустимого контура) произвольных значений аргумента z вне отрезка [- 1, -- 1].

Замечание. Из рассуждений предыдущих пунктов следует, что из всех уравнений Рис 7 48 Лежандра (99) только уравнение с v, равным

целому числу п, допускает ограниченное реше-

ние в замкнутом интервале -1<2;<;1. Это решение единственное, оно совпадает с полиномом Лежандра P {z).

Если значение z = ~~l исключено, то при произвольном v существует единственное конечное решение, совпадающее с P{z).

Решение уравнения Лежандра, стремящееся к нулю при бесконечно возрастающем \z\, дают только функции Лежандра второго рода.

7.6.21. Присоединенные функции Лежандра. Рассмотрим дифференциальное уравнение (98). Подставив в него

f{z) = {i-zy{z), i - )%~-iV+)z + b - V)(y-\-V-)y = - (146)

получим

Положим С= 2

С(1 -C)g-+[(t.+ l)-2(H-ix)C]-(t.-v)(ix + v+l)y = 0.

Это гипергеометрическое уравнение Гаусса. Возьмем его второе решение (пример п. 6.2.10) в качестве определения присоединенной функции Лежандра первого рода. Имеем

W = T0+,(±)V(-v. .+ 1. )

при -1 < г < 4- 1 и

йи=та(1±1Г(- + -

при Z, лежащем вне отрезка [-1, +1]-

Из вида уравнения (98) следует, что Р{-z) также является его решением. Если v-(-{ji.- не целое число, то это решение линейно независимо от Fiiz). Предположим, что это так. Тогда общий интеграл (98) будет

f{z)=AFAz)+BP-:{-z). (147)

В приложениях переменная z обычно вещественна и заключена между -1 и -j- 1; тогда можно положить, что

Z = COS 6.

и окружающую точки ts=~j- 1 и t = - 1 (ко не = z), как показано на рис. 7.48. то криволинейный интеграл

Дифференциальное уравнение (98) относительно новой переменной 6 имеет вид

Если значения 6\близки к О, то общий интеграл этого уравнения

APt (cos б) + ВР (- cos б) будет близок к общему интегралу уравнения

равному СУДб Уу (у+1))4-ОКДе /v(v + l)).

Если v-4-[A - целое число, то решения yif(cos6) и РГ(-cos 6) линейно зависимы, так как эти функции связаны равенством

Р! (cos 6) = (--l) -Р!(-cos 6),

и выражение (147) уже не дает общего интеграла уравнения (98V

Определим присоединенную функцию Лежандра второго рода Q{z) как предел выражения

я PjJ-(cos 6) cos (V + [.t) 71 - (-cos 6)

2 sin(v + j.)OT

при v-4-р стремящемся к целому числу. Легко заметить, что. введенная функция Q(z) бесконечна на обоих концах промежутка [-1, +1]. Следовательно, не существует индексов, для которых уравнение (98) имеет конечное решение в промежутке

-1<2<+1.

Можно также определить присоединенную функцию Лежандра второго рода при любых индексах с помощью разложения в ряд по убывающим степеням переменной.

Положим в уравнении (146) C=z. Тогда оно принимает вид 4!;(1 -C)g + [2-(4fx+6)C]-(t.-v)(t. + v+l)y = 0.

Это уравнение гипергеометрического типа, допускающее в качестве частного решения следующее выражение, которое мы возьмем за определение присоединенной функции Лежандра второго рода при г> 1:

Обычно условия регулярности, которым должны удовлетворять решения уравнения (98), автоматически выполняются при целых индексах v и р,. Соответствующие функции имеют важное значение, и в дальнейшем мы будем рассматривать только такие функции.

7.6.22. Присоединенные функции Лежандра для целых положительных индексов. Предположим сначала, что z вещественное (-1г--1) или соответственно z = cos 6 (О < 6 тс). Сделаем подстановку

/(2) = (1~г2)у(г)