обозначить сумму вычетов относительно полюсов, заключенных внутри окружности С.

Пример. Вычислить

~1 {а

-f- b cos 6)2

(a > 6 > 0).

Имеем

-a + Va~b.

Единственный полюс, заключенный внутри круга радиуса I, z = кратность его равна двум. Найдем вычет относительно этого полюса:

dz \{

dz \{bz + a + Yai - bfl\ -a+V 4

Следовательно,

1.3.22. Интегралы вида jf{x)dx. Пусть f(x) - функция веществен-

ной переменной х, удовлетворяющая следующим условиям:

а) f(z) голоморфна во всей полуплоскости, расположенной над вещественной осью, исключая конечное число полюсов;

б) f(.z) не имеет полюсов на вещественной оси;

в) если \z\ стремится к бесконечности, то zf(z) стремится к нулю равномерно относительно аргумента z, изменяющегося от О до и.

со о

г) jf{x)dx, сходятся.

о -оо

Легко показать, что J f{x)dx pa-

вен 2тгуТ, где £ представляет собой сумму вычетов относительно полюсов функции f{z), расположенных над вещественной осью.

Для доказательства достаточно рассмотреть (рис. 1.33) контур интегрирования, состоящий из части вещественной оси между -р и р и полуокружности Г с центром О и радиусом р, причем р настолько велико, что все полюса А, В, С, ... функции f{z) находятся внутри Г. Если устремлять р к бесконечности, то часть интеграла, соответствующая Г, стремится к нулю в силу допущения в). Следовательно,

Рис. 1.за

J /(х)йх = 27гу£.

+ СО

Положим f (z) = -i-y В z = j рассматриваемая функция имеет

единственный полюс над вещественной осью (его кратность равна трем). Вычет £ относительно этого полюса равен

Следовательно,

({z + jT )

mj

I 3

1.3.23. Интегралы вида j f(x) cos mxdx, j f(x) sinmx dx. Пусть

функция f (z) удовлетворяет условиям предыдущего параграфа, причем условие в) заменено менее обременительным: если \z\ стремится к бесконечности, то f{z) стремится к нулю равномерно относительно аргумента z (О <; arg 2 <; ir). Рассмотрим контур на рис. 1.33. Согласно лемме Жордана имеем (т > 0)

+ 00

где S обозначает сумму вычетов относительно полюсов функции f(z)e, находящихся в верхней полуплоскости. Отделяя вещественные и мнимые части, можем написать

+С +СО

J f (х) cos mxdx = --2:zl01), J /(x)sinmx dx = 2uR(S).

-co -co

Из формулы

+00 +CO

f f(x)e -dxf [f(x)e J-\-f(-x)e- J]dx27jIi

-oo 0

вытекает, что если f{x) - четная функция, то

+ СО

j f(x) cos mxdx -t:j E,

a если f (x) - нечетная функция, то

j fix) sinmx dx с

Приме p. Вычислить

-TOO

= j -:;k2-dx (c>0, fe>0).

Пример. Вычислить

Функция Уг- имеет над вещественной осью только один полюс Z ~ jk. Вычет относительно этого полюса равен

ak

Следовательно.

Замечание. Пусть /(г) имеет простые полюса на вещественной оси, иначе говоря, условие б) п. 1.3.22 не выполняется. Пусть функция fix) такова, что ее интеграл в интервале, где /(х) получает бесконечные значения, сохраняет смысл. Тогда при вычислении интегралов, рассмотренных в п. 1.3.22-23, следует к сумме вычетов S относительно полюсов над вещественной осью прибавить величину ° де о означает сумму вычетов относительно полюсов на самой вещественной оси-

1.3.24. Интегралы вида xf{x)dx, Полагаем, что f{x) - рациональ-

ная функция X, причем z - f {Z) стремится к нулю, когда \z\ стремится

к бесконечности и к нулю, и j (z) не имеет полюсов на положительной части вещественной оси. Если мы осуществим разрез на этом отрезке вещественной оси, то функция z°f{z) будет однозначной на всем контуре, не пересекающем разрез (в частности, на контуре рис. 1.34). Пусть р - радиус малого круга, а /? - радиус большого круга такие, что в полученном кольце содержатся все полюса / {z). В силу предположений относительно f{z) интеграл, взятый по большой окружности, стремится к нулю, если R бесконечно возрастает, а интеграл, взятый по малой окружности, стремится к нулю вместе с р. Следовательно, интеграл, взятый по АВ и DC, равен сумме вычетов £ относи-полюсов функции zf(z), так как вычет относительно г; = 0 В самом деле, z°f( z) стремится к нулю вместе с \z\, и по*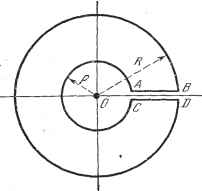

Рис. 1 34.

тельно всех равен нулю.

этому коэффициент при \jz разложения функции zf{z) должен быть равным нулю.

На АВ Z - X, на CD z = хе-К Таким образом,

lim Г [л:-/ (х) - xeif {Л)\ dx = 2иУ S.

Наконец,.

/ x.f\x)dx=~.