се2 {z, q)=2i bIUos 2rz,

сеЛ 1 (2. g) = 2 Bl rtl cos (2/- + 1) г,

se2 +i iz, <7) S 2 +i sin (2r -h 1) z.

se2 +2 iz, q) = 2- l :sin (2r -(- 2) z.

Теперь решения се и se определены с точностью до постоянного множителя Чтобы фиксировать этот множитель, положим, по определению,

2л: 2it

/ [се iz)f dz = f [se (z)] dzrz.

Эти условия аналогичны формулам, справедливым для круговых функций:

2it 2it

J cosx dx= j sittx dx = я.

Отсюда получаем дополнительные соотношения

r=0 /- = 0

Замечание. Коэффициенты A и В зависят от q. Если устремить q к нулю, то из определений функций се(г/ и £е(г;) непосредственно следует

All (0) = Altl (0) = Bi r (0)== Bltl (0) = 8

где - символ Кронекера.

*) Рекуррентные формулы относительно А fi В приведены в [8] на стр. 383, 384 отдельно для каждого из разложений (168).

Подставим это разложение в уравнение (164). Тогда получим два рекур-рентныл соотношения одинакового вида: одно, связывающее три коэффициента А, другое - три коэффициента В, индексы которых отличаются на две единицы. Например, для коэффициентов А имеем *)

(а-г2)Л,.-д(Л,+2+.-2) = 0. (167)

Отсюда находим четыре возможных разложения для функций се и se . Коэффициенты этих разложений, очевидно, зависят от значений т, поэтому они снабжены верхними индексами. Имеем

7.7,4. Характеристическое уравнение. Применение рекуррентной формулы (167) позволяет написать характеристические уравнения (165) и (166) в виде сходящихся непрерывных дробей i). Мы приведем только окончательные результаты:

2 1 4 -й

4г2-

(169)

a = q-\- 1

q I

9 -fl

0 = 4

16 -e

-K2r+V- - {2 +i(c. g) = 0}, (170) -\(2r + 2f-l- {Ф2 +2(с. g)-0}. (171)

,9- -,(2r-f-lV-J---- {Ф-( (172)

Пример. Приведем пример использования предыдущих формул для вычисления пары возможных значений с, q.

с= -9+1 -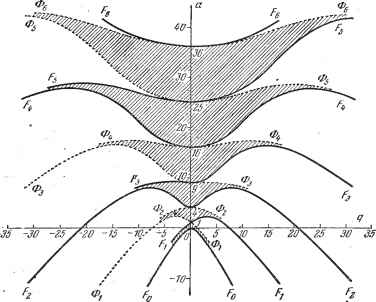

Рис. 7.55.

Пусть требуется вычислить значение а, соответствующее д = 2, чтобы уравнение (164) допускало в качестве решения сед (г). Это значение а представляет собой ординату точки пересечения прямой q - 2c криврй (с, q) = 0. Кривая F{a, q) = 0 (рис. 7.55) пересекает ось а в точке а = 9. Поэтому искомое значение а близко к 9. Уточним его с помощью (170).

) По типографским, соображениям непрерывная бесконечная дробь

записыв<1е1си з виде fcj, + -j- + j- +

b2 +

3) Корни. Функция se обращается в нуль при 2 = 0, функции se2 и се2 +1 равны нулю при z = . Функции sCj+p se2 +2 2п in+i имеют,

кроме того, п корней в интервале 0, . Эти корни приближаются к

по мере роста q). Наконец, функции se(2) и се(г) между О и тс имеют такое же количество корней, как sin/иг и cos mz.

7.7.6. Присоединенные функции Матье первого рода. Если в (164) заменить Z на jz. то это уравнение принимает вид

-~{a - 2q ch 2z) у = 0.

Для значений с, удовлетворяющих равенствам (169) - (172), существуют решения с периодом 2тс/. Они называются присоединенными функциями Матье первого рода и обозначаются Се и Se . Эти функции, очевидно, связаны

Ce (2) = ce(i).

Se (2) = -yse (y2).

) В [8] на стр. 386 и последующих приведены рельефы функций у = сео, се sei, сег, sej (х, д) в системе координат х, д, у. В книге [28] имеются графики первых функций се , se j для различных пар qua.

В правую часть равенства (170), оборванного при г~2, подставим q - 2. с =9,4 и q=2, <7 = 9,3. Тогда левая часть (170) соответственно равна Cj=9,l и 2= 10,21 и линейная интерполяция приближенно дает Сз=9,37.

Подставим теперь в правую часть (170), оборванного при /-=3, значения 9 = 2, а = 9,37 к q=2, с = 9,38. Тогда леваячасть дает соответственно ci = 9,373 и С2= 9,272. С помощью линейной интерполяции получаем аз = 9,3731. Значение 9,373 дает хорошее приближение величины а. .

Рассмотренным выше способом можно по точкам построить кривую F.,{a.. g) = 0.

7.7.5. Поведение функций c&m(z, д), sem{z, д). 1) Симметрия относительно Z. Функции се(г, q), se{z, q) имеют период и характер симметрии такие же, как функции cos z, sin z, если m - нечетное число, и cos 2z. sin 2z, если m - четное число.

. 2) Симметрия относительно q. Если в уравнении (164) заменить q на - 9, а 2 на - 2. то оно сохраняет первоначальный вид

-g- + [c-2gcos22]y = 0.

В силу симметрии функций и Ф относительно q имеем