(218)

22fe-l

если п = 2ft;

(2*4-1) , , ,

--\ , если й=2Л-К1.

Функции Чебышева второго рода t/ могут быть представлены следующими формулами:

t/ (co)= ± /l - со2 /7 (ш). если со<1; t/ (co)= ± УсоЗ- 1 /7 (со), если со > 1, где Г (ю) - полином ( -1)-й степени от со. Выражение для / (со) будет

/; (со)=2 jco--172 +

(я-3)(п-4) я (п-4) (я-5) (я-6)

2!2* 3!26 со -t- ...

Последний член в квадратных скобках равен

rt-i я - 2 rt-J

22fc-

Y со, если п = 2ft;

если = 2ft--I-

22fc

Полином Р (ш), равный р +1(ш). называется полиномом Чебышева второго рода.

Отметим, что эти же результаты можно легко получить, если применить к дифференциальному уравнению метод, указанный в п. 6.2.10 (искать

Функции Т и t/ называются соответственно функциями Чебышева первого и второго рода ге-го порядка.

Функция / (ш) представляет собой полином. Действительно, при ш < 1 имеем

Г (ш) 4- 7t/ (ш) = (cos 14- J sin tf = (со ± у;~Т)\ Г (ш) - 7t/ (CD) = (cos t ~ J sin 0 = (ш + /0)2 - 1) . Отсюда

Тп (< )I± /i;) + + (218a>

При )ш > 1 имеем

Тп ( >) - t/ (со) = е- = (со + Ко;) .

ЧТО приводит для / (со) к тому же соотношению (218а).

Полином 7 (со) называется полиномом Чебышева первого рода.

Если при помощи формулы бинома разложить выражение (218а), то-найдем

/ ( )> - О) 1122 212 3!26

Последний член в квадратных скобках равен

(220)

7.9.2. Графики 7 (о>) и (ю). Если мы вернемся к формуле (214), то легко увидим, что гра(})ик полинома Чебышева Г (о)) в интервале (-1, +1)

представляет собой проекцию синусоиды с периодом - и амплитудой единица, обвитой вокруг цилиндра вращения с радиусом единица, на плоскость, параллельную оси цилиндра (см. рис. 7.56). Один из максимумов или минимумов синусоиды находится в плоскости, параллельной плоскости проекции и проходящей через ось цилиндра. Изучаемая проекция представляет собой частный случай кривых Лиссажу. Каждая точка кривой является проекцией двух точек, симметрично расположенных на цилиндре. Это соответствует тому, что согласно (218а) функцию Т (ш) можно представить как полусумму проекций двух комплексно сопряженных точек. На рис. 7.56 изображен полином Т, представляющий собой проекцию шести периодов синусоиды, обвитой вокруг цилиндра.

На рис. 7.57 приведены графики шести первых полиномов Чебышева. Они выходят из (-1) со для отрицательных и очень больших ш, колеблются п-1 раз между абсциссами и ординатами -1 и +1 и быстро возрастают

-к + со для О) > I. . .

решение в виде обобщенного степенного ряда). Первые одиннадцать полино-мов Т и /? следующие:

Го(ш)=1.

(ш) = 2а)2 - 1, Ts (ш) = 4u)3 - 3(1), Г4(ш)=8<о4-8io2+l,

(о)) = 16а)5 - 20а)3 -j- 5ш, (219)

Tg (ш) = 320)6 - 48ш418а)2 1,

ГЛU)) = 64ш7 - 112ш5 4- 56(1)3 - - 7 . T-g (ю) = 1280)8 - 256а)б-{-160(1)432(о21, 7-5(0))= 256(1)9-576ю7-{-4320)5- 120а)3-{-9а), . TjqC ) = 512о)10 - 1280о)8-I-1120(1)6 - 400о)4 4-50о)2 - 1.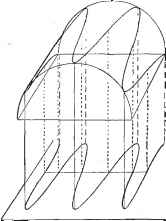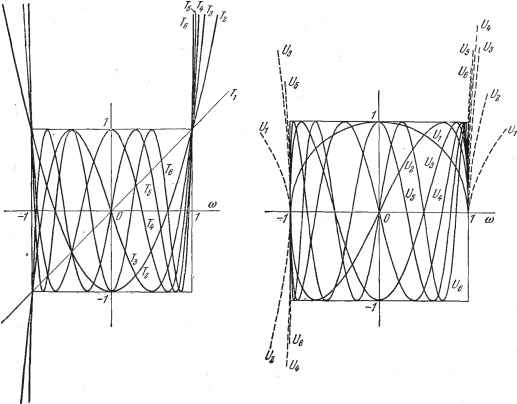

Рис. 7.56.

Рис. 7.57.

Рис. 7.58.