
 | |
|
Главная
>
Дифференцирование и интегрирование по аргументу Пример. Вычислить Функция f(z)= +z) имеет два полюса второго порядка z=±Ji -fu (-1<а<3). о 1 2( -1) Следовательно, 1-я l-ej а - 1 -ч - 1 4у -/ /2 4/ -/- /2 1 е2/< 4 COS 71/2 1.3.25. Применение теоремы о вычетах к суммированию некоторых рядов. Рассмотрим ряд +(Х> п = -оо Положим, что функция fiz) голоморфна на всей плоскости z за исключением нескольких полюсов а, , а, вычеты относительно которых равны bi, .... бд,. Контур С заключает в себе все полюса f(z) и точк:? О, + 1, ± п вещественной оси. Числа Cj, а, разумеется, не целые, так как иначе ряд не имел бы смысла. Рассмотрим функцию ср (z) = т ctg тег/(г), ко- fiJfJ) торая внутри контура С имеет в качестве полюсов полюса / {z) с .вычетами -кЬ ctg-ка, Tcftg ctg гсг .... тгб J ctg и точки О, + 1, ..., ± /г с вычетами /(0), /(±1), f(±n). Имеем ~ f ср (Z) dz = {/(- )+/( й + 1) + ... Если контур С при бесконечно возрастаю- Рис. 1.35. щем п отодвигается в бесконечность, причем криволинейный интеграл функции (р(2) по С стремится к нулю, то можно вычислить сумму рассматриваемого ряда. Эти условия соблюдаются, если, например, в качестве контура С использовать квадрат, пре.аставленный на рис. 1.35, и считать, что при бесконечном возрастании \z\ произведение zf {z) равномерно стремится к нулю. Выберем п достаточно большим, чтобы п/{п)<:г\ ctgscz ограничен на С , пусть М - его верхняя граница. Тогда справедлива оценка / zfiz)dz < 471£Ж (2/2 + 1) /г+ 1/2 Следовательно, контур С отвечает поставленным условиям и + сг. S /( ) = -it ctg ufli+- ... bi,ztgT.aj,\. Пример 1. Вычислить -а Функция 22 стремится к нулю. когда 11 бесконечно возрастает. Функция 2 не имеет полюсов при значениях z, равных целому числу, и голоморфна на всей плоскости, за исключением г = ± ja. Следовательно, =i+2 5;-у=-u {ctg + Ctn Uft. Значит, cth тса. Замечание. Если вместо ctgnz использовать условиях можно суммировать ряды вида со П= -со П р и м е р 2. (-1) 1 i 1 ,г2 1 а2 Т 2й sh таг * то при тех же 1.4. КОНФОРМНЫЕ ОТОБРАЖЕНИЯ L4.1. Определение. Дана аналитическая функция Z=f{z). Если точка т с аффиксом z = х -\- Jy описывает кривую т в плоскости z. то точки М с аффиксом Z-X~\-JY описывает кривую Г в плоскости Z Рис. 1.36. 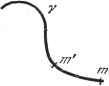 (рис. 1.36). Кривая Г называется образом кривой у, точки Мит называются соответствующими. Основное свойство этого преобразования состоит в том, что оно сохраняет углы и, сле,аовательно, вид бесконечно малых элементов. Поэтому оно называется конформным (conforme - подобный). Действительно, пусть т, т - две соседние точки на кривой у, а М и М - две соответствующие точки на кривой Г. Если обозначить через (f) и Ф углы между mm и Ох и между ММ и ОХ, то В этих формулах mm и ММ означают длины соответствующих отрезков. Если т стремится к т, то М будет стремиться к М. Можно показать*), что при этом отношение длин стремится к \f{z)\, а угол поворота (Ф - (р)-к аргументу производной функции f {z). Таким образом, dZe \f{z)\dz.- Это означает, что при конформном отображении элемент dz удлиняется в j/(2) раз и поворачивается на угол arg/(г). Такое же преобразование испытывает любой бесконечно малый элемент компяексной плоскости. Если Y] и Y2 - две кривые в плоскости z, проходящие через точку z. и образующие друг с другом некоторый угол, то такой же угол по величине и по знаку образуют между собой образы этих кривых Г, и Т. Проведенные рассуждения перестают быть верными в точках, где производная равна нулю или где ее модуль бесконечен. Действительно, рассмотрим, например, функции Z = kz (пу- 1) и Z = - (см. случаи а) и г) п. 1.4.2). Две прямые, проходящие через начало координат и образующие между собой угол ср, преобразуются в плоскости Z в две прямые, образующие между собой угол пф (случай а) и - ср (случай д). В первом примере модуль производной в начале координат равен нулю, во втором - бесконечности. Отделяя в равенстве Z = f (z) вещественные и мнимые части, получим Z=X-+-jYf(x-\-Jy) = Xix, у) + уТ(х. у). Если точка Z описывает кривые X {х, у) = const или К (л:, у) -const в плоскости г, то точка Z описывает прямые, параллельные осям OY, ОХ (рис. 1.37 ). Следовательно, в силу сохранения jrrлов кривые (х, у) = const Рис. 1.37. и Y{x, у) = const ортогональны, (х, у) и К(х, у) - вещественная и мнимая части f (z)-называются сопряженными функциями. Часто бывает проще рассматривать не Z = f{z), а обратное преобразование z = F (Z). Приравнивая вещественную и мнимую части, получаем х = х(. К), у==у(Х, Y). *) Подробнее см. [1], стр. 96-99.
|