-1 / F (S) ds С / dx. . . (24).

Произведем предыдущее интегрирование от 1 до бесконечности. При той же замене переменных находим

}fFis)dscf±dx. ; (25)

Проинтегрируем го р от нуля до бесконечности обе части равенства (21). Так как -

fe-Pdp=\,

получаем равенство

fFip)dp = f. (26)

) Дифференцирование по параметру k обеих частей

F(j?,k)c:h(t,k)

сводится, исходя из определяющей формулы (21), к дифференцированию под знаком интеграла. Новый интеграл сходится, т. е. dh/dk имеет изображение, если только условия, оговоренные в п. 8.3.1, выполняются.

) Интегрирование по параметру k обеих частей равенства

F(p.k)c:h(Uk) . -

.сводится, исходя из формулы (21), к изменению порядка интегрирования

к, со

j dk e-Ph(t, k)dt, . ...

со Й2

ЧТО возможно, если интеграл е~Р* dt h(t, к) dk существует.

Продифференцируем соотношение (22) по k. Это допустимо *), потому что k -параметр, не зависящий ни от р, ни от t. Получаем

F{kp) + kpF{kp)\Z-yh(y

Если положить = 1,. то ,

4p\pPiP)\-th{t), 423)

Разделим выражение (22) на ft: ...

Pikp)nh[).

Проинтегрируем 2) обе части по ft от О до I:

о о . .

Положим s~kp, а х = . Тогда

8.3.4. Дифференцирование функции h{f). Умножим на р обе части преобразования Лапласа и проинтегрируем по частям. Получим

оэ оо

т. е.

pF(p) - h(0)\Zh(t). (27)

Повторив п раз тот же прием, получаем последовательным интегрированием по частям

рпр (р) рп-11г (0) - рп-Ч (0) - ... - /7й< -2) (0) /г(п-1) (О) □ /г* {t). (28) Если h{0) - 0, то выражение (27) принимает вид

pF{p)\Zhit). (29)

Если /г (0) ==/г(0) = ... =/г( 1)(0) = 0, то выражение (28) преобразуется в

p F{p)\Zh 4t)- (30)

8.3.5. Интегрирование функции h{t). Найдем изображение функции

h{t)dt. Согласно формуле преобразования Лапласа, это изображение равно

fe-P /МО

Интегрирование по частям дает

оо- г г

fe-P f h(t)dt dt= -e-P* f h(t)dt 6 Lo -1 L 6

iXJ CO

+ у/ e-h{t)dt*) = ±- f e-Phit)dt.

Следовательно,

cf hit)dt.

Tot же прием, повторенный n раз, дает

It I

dtfdt... fh{t)dt.

(31)

(32)

0 0

Формулы (30) и (32) показывают, что дифференцирование и интегрирование функции h{t) приводит соответственно к умножению и делению изображения F{p) на р.

*) Здесь следует учесть, что

lim е-

t->+co

e-Pt h{t)dt = 0. . о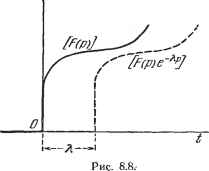

Аналитические операции над h{t) приводят к алгебраическим операциям над F{p). Этим объясняется громадное упрощение, которое вносят в анализ приемы операционного исчисления.

8.3.6. Теорема смещения. Дадим переменной р приращение X. Тогда преобразование Лапласа примет вид

. Ш) fi-

F{p-\--k)= \ e-pt~>th (t)dt. о

F{p-\-\)== I e-pte-h (t) dt.

Отсюда

F{p + -k)Ce-h{t). (33)

8.3.7. Теорема запаздывания.

Вычтем из аргумента t положительное число X. Функций h{t), или, точнее, функция h{t)T{t) (так как Y(t) всегда подразумевается), преобразуется в /г(/~Х)Г( -X) (рис. 8.8).

Заменим t на t - X в преобразовании Лапласа:

F{p) = j hit - X) е-РеР dt л

или, введя множитель Х(/-X) и разделив на еР,

e-PF{p) = fhit - K)r{t-l)e~Ptdt.

Нижний предел интегрирования может быть взят равным нулю, так как из-за присутствия Y( -X) вклад интервала (О, X) равен нулю. Отсюда

e~>-PF (р) = f h(t~l)Iit - X) e-pi dt

и, следовательно,

e->-PF (р) С /г ( - X) Г ( - X). (34)

В случае, когда h{t) равна единичной ступени, мы имеем (рис. 8.9)

Рис. 8.9.

J e-xp-x(f Х).

(35)

8.3.8. Дифференцирование функции F{p). Продифференцируем по р обе части формулы преобразования Лапласа. Получаем

Р(Р)= / -th{t)e-P0.

Отсюда

(36)

F{p)C~thit). Продифференцировав п раз, получаем

Р (i; L (-1) /г (О ( - Делое положительное). (37)