создаст в контуре т. ток Ri{t). По примеру п. 8.2.1 можно показать, что достаточно знать функцию R, иначе говоря, импульсную реакцию контура т на контур Z, чтобы определить ток l{t), текущий в m в результате приложения к I любой электродвижущей силы, равной нулю при < 0. £С()

Вместо того чтобы разлагать функцию Efnt) E{t) на ступеньки, как на рис. 8.4, разложим ее на вертикальные полосы (рис. 8.11). £(jut) Каждая часть Е (t) будет при этом заклю- E(Zut) чена между двумя импульсами щириной в Lt. 6CAtj Обе определенные таким образом ступен- чатые функции будут стремиться к E{t) при Lt, стремящемся к нулю, при условии, если Eijt) не имеет резких скачков.

Каждая элементарная реакция будет равна

E(0)Rit), E{M)Rit - M)., E(2M)Rit - 2M), ...

Ток i(t) будет представлять собой сумму этих элементарных реакций.. Поэтому

i(t) = j E(z)R(t - z)dz= j E(t - z)Riz)dz.

(12) показывает, что импульсная реакция контура т на кон-с обобщенным взаимным сопротивлением соотношением

At М М

Рис. 8.11.

Формула тур / связана

Применение формулы обращения

8.3.22. Теорема Меллина - Фурье. Мы видели (п. 1.3.15). что единичная ступень может быть выражена интегралом

+joo

c+jco

- со

Контур интегрирования представляет собой

f-oo

Рис. 8.12.

-joo c-jca

Рис. 8.13.

вещественную ось с маленькой полуокружностью (рис. 8.12), Положим; /ш = р. Тогда

+]со

-уоо

При этом контур интегрирования представляет собой мнимую ось с маленькой полуокружностью, как показано на рис. 8.13. Он может быть заменен любым другим контуром Г, соединяющим точки - уоо и -1- joo и расположенным справа от мнимой оси. Действительно, согласно теореме Коши, так

как между мнимой осью и Г функция - не имеет особых точек, мы можем написать

+ /00

-/с (Г)

Контур г может быть, в частности, прямой, параллельной мнимой оси с положительной абсциссой с (контур Бромвича). Следовательно,

C+JCO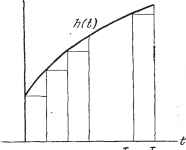

О т:7 г 3 -/7-7 Рис. 8.14.

dp.

(82)

C-JCO

Установив это, рассмотрим функцию h{t), изображенную на рис. 8.14. Повторив рассуждения, сделанные при выводе формул (1) - (6), мы можем разложить эту функцию на ступеньки:

/г (0) Г (О + 1 [/г (т ) - h (t: i)] Г (г - т ).

Если устремить это выражение к пределу, бесконечно уменьшая промежутки т - Cn-i. ступенчатая кривая будет стремиться к* кривой hIJ:), и тогда

+ 00

Заменим в этой формуле - -с) выражением (82). Получим

hit):

27су dt f f

pP 4-t:i

-dph {z)dz.

0 с- joo C+Joo

> = W-i- / ~f.-hi.)d.dp.

c-joo 0

Отсюда, пользуясь формулой преобразования Лапласа, найдем

C+Ja>

г yj. Id

ePtPip)

T. e.

c- joo c+joo

hit)

=w / Pip)dp-

c-joo

(83)

Мы получили формулу обращения. Ее называют формулой Меллина - Фурье.

с- JCO

Таким образом, h{t), неявно выраженная интегральным уравнением

F(/,) = J h{t)e-Pdt, . (84)

дается в явном виде формулой (83) через интеграл по простому контуру в плоскости комплексной переменной р. Если этот интеграл равен нулю вдоль бесконечной полуокружности, находящейся слева от контура (п. 1.3.19), то его вычисление сведется к простому вычислению вычетов при условии, что особые точки являются полюсами или существенно особыми точками. Если же особые точки являются точками разветвления, то это вычисление сведется к интегрированию по эквивалентному контуру.

Формулы (83) и (84) эквивалентны. Можно применять любую из них. Нужно, однако, заметить, что формула (83) более общая, чем формула (84), и может дать результат, даже если формула Лапласа приводит к расходящемуся интегралу.

В качестве примера найдем с помощью формулы (83) некоторые выражения, уже полученные раньше с помощью формулы Лапласа,

Пример 1. Найдем оригинал -рр (п - целое положительное число).

Формула обращения (83) дает

c+jco . .

с-joo

Из первого примера п. 1.3.19 известно, что значение этого интеграла t

Мы снова находим уже известное выражение

1 t

Пример 2. Требуется найти оригинал р2д2 Применим теорему обращения. Искомый оригинал /г(0 имеет вид

c+jco c-jco

Вычисление (см. п. 1.3.12) дает й(0=-~- . а это приводит к уже

1 1

известному выражению -sin □

а р + а

8.3.23. Замечания о применении формулы обращения. Мы доказали с помощью преобразования Лапласа формулу (56):

1. .

p.+i ~ r(v + l)

Эта формула, где v-вещественное число, была доказана для случая, когда v > - 1. Если v < - 1, интеграл Лапласа не сходится. Докажем теперь формулу (56), применяя теорему обращения.

Рассмотрим функцию /(/?). Это изображение h{t), определенное формулой преобразования Карсона. Имеем

с+700