68 ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ

в этом случае кривые, которые преобразуются в прямые, параллельные осям ОХ, 0Y, задаются в параметрической форме: Y фиксировано, X меняется или X фиксировано, Y меняется.

Исключая из обоих равенств последовательно X и Y, получим соответственно

g{x, у, К) = 0, h(x, у, Х)=0

-уравнения семейств кривых, преобразующихся в параллели осям ОХ и OV, причем Y а X играют здесь роль параметров, фиксирующих конкретную кривую.

Из аналитичности f{z) следует (см. п. 1.3.3), что

дх + дх ду

Таким образом, функции Х{х, у) и Y{x, у) - гармонические, причем семейства Х{х, у) = const и Y\x, у) = const ортогональны в плоскости z. Эти семейства ортогональных гармонических функций преобразуются в семейства прямых, параллельных осям координат плоскости Z.

Отметим, что эадача отыскания функции Z - f iz), отображающей кривую y - vjix) плоскости Z в прямую, параллельную какой-нибудь оси плоскости Z, в общем случае не рещается. Поэтому обычно приходится ограничиваться заранее известными конформными отображениями, используя ортогональные семейства двухмерных гармонических функций (например, отображения при помощи комбинаций элементарных функций). Эта задача отыскания ортогональных семейств двухмерных гармонических функций возникает при рассмотрении различных плоских полей.

Примеры: 1) отыскание. силовых и эквипотенциальных *) линий электростатического или магнитного плоского полей; 2) отыскание линий теплового потока и изотерм нагретого тела; 3) отыскание линий равного потенциала скорости и линий тока плоского установившегося движения жидкости; 4) отыскание линий электрического тока и эквипотенциальных линий в проводнике и т. д.

Рассмотрим подробнее случай электростатики. Пусть даны два проводящих тела, помещенных в идеальный диэлектрик. Их потенциалы соответственно Vj и Vg- Основная задача в этом случае состоит в определении конфигурации возникшего электростатического поля и величины заряда на каждом из проводников. Известно, что эта задача сводится к отысканию решения уравнения Лапласа, т. е. к отысканию гармонической функции, которая принимает заданные величины V- и Kg поверхности проводников. Если проводники представляют собой два цилиндра с параллельными осями, продольные размеры которых велики по сравнению с поперечными, то, изучая распределение поля в поперечном сечении средней части проводников, можно пренебречь краевыми эффектами. Таким образом, мы приходим к плоской задаче.

Если мы найдем конформное отображение, приводящее поперечные сечения цилиндров, изображенные в плоскости z, в соответствие с параллелями X = Vx, X-V2, изображенными в плоскости Z, иначе говоря, если нам удастся задать оба этих поперечных сечения в качестве представителей некоторого семейства гармонических функций, то прямые Y = const и Х=: const являются соответственно образами электростатических силовых и эквипотенциальных линий, расположенных в плоскости z. В частности,

*) Линии равного потенциала или линии уровня.

1.4] КОНФОРМНЫЕ ОТОБРАЖЕНИЯ 69

К эквипотенциальным линиям относятся и поперечные сечения данных цилиндров, значения потенциалов на которых как раз равны V, и Vg-

И обратно: если задано какое-либо конформное отображение Z - /(г), то с помощью функций X (х, у), V(x, у) можно решить соответствующую электростатическую задачу. Мы уже отмечали, что вычисления в этом случае гораздо проще, чем в предыдущем. Выражения Х (х, у) = const и Y{x, у) = const представляют собой уравнения эквипотенциальных и силовых линий.

Остается определить плотность заряда о и величину заряда q проводника Пусть Е-вектор электрического поля; он является градиентом скалярного потенциала. Если принять функцию Х{х, у) за потенциальную функцию, то (п. 3.2.16)

E=zgX2tUX{x. у).

Обозначим через е диэлектрическую проницаемость среды. Известно, что поверхностная плотность электрического заряда о равна произведению s на модуль вектора Е в рассматриваемой точке поверхности проводника. Так как этот вектор нормален к поверхности, то

дХ дп

или в силу ортогональности кривых X и V будет

дГ ds

Рассмотрим элемент нашей цилиндрической поверхности, имеющий высоту единица и стягиваемый дугой длиной ds. Заряд, несомый этим элементом, равен

dq - ads - edV.

Заряд участка поверхности единичной высоты, опирающегося на дугу АВ поперечного сечения цилиндра, равен

q = sf dV = eiY-Y).

Заряд единицы длины одного из цилиндров (единичный заряд), который мы определим, если совершим полный поворот вокруг соответствующего поперечного сечения, равен с точностью до коэффициента е приращению функции Y. Если цилиндр заряжен, эта функция, очевидно, неоднозначна.

В нижеследующих примерах обе функции Л и К взаимно заменяемы и одна из них, в зависимости от условий, играет роль функции потенциала.

Пример. Рассмотрим преобразование Z = arch > т. е. z - d ch Z.

Имеем

x = dchXcosY, y = dsh XsinY. Если считать X постоянным, то в плоскости z получаем кривую

jt:2 , У--

- 1=0.

) Мы используем рационализированную систему единиц. В нерационализиро-ванной системе достаточно заменить в нижестоящих формулах а на 4яа и на q. По поводу рационализированной системы см. сноску на стр. 147.

Если считать V постоянным, то в плоскости z получаем кривую

d cos Y d sin2 Y

1 = 0.

Эти кривые образуют ортогональные семейства эллипсов и софокусных гипербол с фокусами F и F, отстоящими друг от друга на расстоянии 2d.

Рассмотрим эллипсы и гиперболы соответственно как эквипотенциальные и силовые линии некоторого плоского электростатического поля. В пространстве эквипотенциальные поверхности представляют собой эллиптические цилиндры. Поперечное сечение их изображено на рис. 1.38.

Ничего не меняя в распределении поля, можно материализовать одну из этих поверхностей в виде проводника определенного потенциала. Таким

образом, мы определим силовые линии и поперечное сечение эквипотенциальных поверхностей для наэлектризованного эллиптического цилиндра. В частном случае = 0 наш цилиндр вырождается в плоскую ленту шириной 2d. Указанные выше формулы позволяют и для этого проводника определить силовые линии и эквипотенциальные поверхности.

Определим емкость единицы длины передающего кабеля, у которого внутренний и внешний проводники представляют собой соответственно ленту и эллиптический цилиндр. Если через а Yi b обозначить полуоси эллипса, то - &2 = (2. При обходе вокруг одного из проводников функция У изменяется на 2и. Следовательно, искомая единичная емкость С будет равна i)

где и Х - соответствующие потенциалы ленты и цилиндра. Поскольку Al = 0, а ch Х2 - , для С получим

2ле 2ite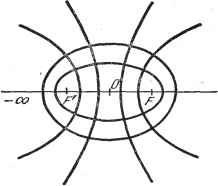

Рис. 1.38.

arch - d

W(a+b)~lnd

Рассмотрим теперь случай, когда гиперболы - эквипотенциальные линии, а эллипсы - силовые линии. На рис. 1.88 изображены эти линии, вызванные в данном случае электрическим полем, возникающим между двумя поверхностями гиперболического цилиндра, наэлектризованными до определенного потенциала. Рассмотрим, в частности, вырожденный гиперболический цилиндр, соответствующий тем значениям V, которые обращают в нуль sin К. Он сводится к двум полуплоскостям, разделенным разрезом шириной в 2d. Ограничим эти полуплоскости прямыми, перпендикулярными FF, с абсциссами х и -X, и прямыми, параллельными оси FF, на расстоянии / от нее (рис. 1.39). Конечно, чтобы не возмущать поле, остальная часть каждой полуплоскости должна обладать тем же потенциалом, но по контурам ABCD

) В нерационализированной системе единиц следует правую часть формулы для емкости С разделить на 4л.