i(t\ - р (l j e k:r] ~:re

Примечание. Если бы требовалось найти выражение i{t) при < то функция S (р) была бы изображением бесконечной синусоиды у , так как при < ~ Цепь не знает , что эта синусоида будет прервана в момент t = - .

8.3.27. Изображение периодических разрывных функций. Пусть h (t) - однозначная функция с периодом К начинающаяся в момент f = О, не принимающая бесконечных значений и имеющая конечное число разрывов, максимумов и минимумов в периоде (рис. 8.20),

Пусть F (р) - изображение О \ / 1 \ J Z \ / л \ функции h{t), а (р) - изобра-

о t жение одного периода этой функ-

PiiSa начинающегося в f = О, т. е.

нулевого периода. Тогда изображение первого периода равно Р{р)еР, изображение второго периода равно Fo(P)~P.....изображение и-го периода равно Ео(р)е р. Отсюда

11=0

F(P)= (86)

Примечание. Применяем теорему обращения:

C+Joi

2nj J 1-e-p

C-JU>

Это выражение дает разложение в ряд Фурье функции й СО-Прим е р 1. Требуется найти изображение и разложение в ряд Фурье функции (рис. 8.21)

h(t)=\smt\.

Найдем изображение нулевого периода этой функции. Изображение синусоиды X (jt) sin t равно p i Изображение синусоиды Г ( - тг) sin {t-ic) равно е~Р

pijl Следовательно, изображение нулевого периода функции h(J:) равно

-i+e-P)..

Применяем формулу обращения

£оС Г еРрЬ+е )

с- jco

Вычеты, соответствующие полюсам±уш, равны нулю, так как I -\- е~~0. Вычет, соответствующий полюсу/> = - -j, дает искомый ток

По формуле (86) изображение функции h(t) равно

1 t + g-P

Разложение в ряд Фурье-функции h(t) будет иметь вид

С+joo

C-JO

Вычеты, соответствующие полюсам р = ±j, равны нулю, так как 1 -\-е-=0. Имеется бесконечное число простых полюсов, удовлетворяющих уравнению

1 - е-Р = О,

иначе говоря, полюсами будут точки p = 2nj, где п принимает целые значения от -оо до Ч~оо. Для полюса р = О имеем

ePilJf- е-Р)

р = 0

еР (1 + е-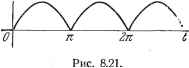

L (24.1)е-Д ipo

Для полюсов, соответствующих всем целым положительным и отрицательным значениям п, кроме нуля, имеем

-1-со со

2 У eJ 4 cos2nt

n=-CO n=l

Отсюда получаем разложение в ряд Фурье:

Isinl =-

, cos 2nt ~Zi 4n-l

Пример 2. К катущке самоиндукции с сопротивлением прикладывают напряжение, равное попеременно -)-£ или -Ев течение промежутков времени, равных Т (рис. 8.22). При пТ это напряжение остается равным ±Е

Рис. 8.22. .

в зависимости от четности или нечетности п. Требуется вычислить ток, проходящий по катущке в момент t, более поздний, чем пТ. Изображение напряжения равно

т. е.

1 .- + (-1) -

2 1+е-Р

Обобщенное сопротивление катущки с сопротивлением равно

Поэтому искомый ток будет

с+Уоо

Е с , 2Е

2J J p(Lp + R)

c-jco

C-JCO

c+jco

f gpg-p?- [1+(-1) + g- p ] dp

Для второго интеграла должны быть рассмотрены полюсы

Р = щ, р:

а для первого интеграла - только два последних. Так как

- Те

= 0,

I2k+1)-Kj

ТО следует принимать во внимание только полюсы р Ток l{t) может быть написан в виде

--и /7 = 0.

t > пТ.

Примечание. Если число зубцов кривой напряжения бесконечно, то это выражение справедливо при

nT<t<i(n-i)T.

При п - 0 мы приходим, естественно, к примеру 1 п. 8.3.13.

Таблица соответствия

8.3.28. Введение. Решение физических или математических задач с помощью операционного исчисления, как уже говорилось, содержит три фазы.

Первая состоит в переходе от реальных данных (переменная t) к операционной записи (переменная р) при помощи формулы преобразования Лапласа

Вторая представляет собой ряд вычислений, приводящих к решению поставленной задачи в операционной форме:

Р{р)Ф(р).

Третья состоит в переходе от операционной записи к реальной (переменная t). Общая формула, применимая к такому переходу, - это, очевидно, формула обращения

Ф(Р)С72(0.

Первая и третья фазы сильно облегчаются существованием таблицы, содержащей преобразования наиболее часто встречающихся математических выражений, и применением правил операционной алгебры, если искомые функций не находятся в таблице соответствия. Это помогает избежать вторичного выполнения вычислений, которые были сделаны по крайней мере уже один раз.

Так как третья фаза вычислений (переход от переменной р к переменной t) всегда наиболее затруднительна, то нам показалось разумным сгруппировать непрерывные функции по семействам переменной р. Напротив, разрывные функции *), которые входят чаще всего в первую фазу исчисления, были сгруппированы по семействам функций переменной t.

*) Имеются в виду случаи, когда функция ила ее производная терляг разрыв.