событий А,

А осуществится, равна

l+ 2+ + 5

Р1 + Р2 +

Ps

В этом состоит теорема сложения вероятностей.

Пример. Вернемся к первому примеру с урной. Какова вероятность при извлечении за один раз двух щаров получить один черный и один белый щар?

Безразлично, извлечены ли оба щара из девятнадцати за один раз. или один щар из девятнадцати в первый раз и потом еще один из восемнадцати во второй раз. При этом могут произойти два благоприятных несовместных события:

1) в первый раз извлечен белый щар, во второй раз черный;

2) в первый раз извлечен черный шар, во второй раз белый.

. Вероятность первого события на основании теоремы умножения вероятностей равна

19 18

Вероятность второго события по аналогии равна

7 12 ТЭ 18

Искомая вероятность будет на основании теоремы сложения вероятностей равна

12 7 12 28

18 + 19

9.1.4. Формула Стирлинга. В полученные выше формулы часто входит величина п\, прямое вычисление которой при больших значениях п требует больших затрат труда и времени. Для упрощения этих вычислений часто пользуются приближенной формулой Стирлинга, точность которой возрастает с возрастанием числа п (асимптотическая формула).

Для вывода этой формулы рассмотрим площадь, заключенную между осью X, кривой у - \пх и прямой, параллельной оси у в точке с абсциссой х - п (рис. 9.1). Эта площадь выражается интегралом

In X dx.

Интегрируя по частям, будем иметь

j \пхdx = nln/i - -J- 1.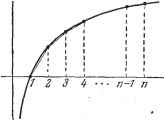

Рис. 9.1:

С другой стороны вычисляя этот интеграл приближенно по формуле трапеций, получим

J lnxdx= + 4-1п2Ч- ... --1п(/г-1)=1п/г! -у1п .

*) Теорема сложения вероятностей обычно формулируется так: вероятность суммы несовместных событий равна сумме вероятностей этих событий. При этом суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий (в случае несовместных событий суммой нескольких событий называется событие, состоящее в появлении одного из этих событий).

или

/г! да /г-f-yj In - п, откуда для п ! получаем приближенное выражение

Таким образом, можем написать

и! = /г е- ]/ ср( ). (1)

Покажем, что функция f(n), компенсирующая ошибки приближенной формулы, при и, стремящемся к бесконечности, имеет предел и предел этот равен /27г.

Действительно, рассмотрим соотношение

?( )

Имеем

\ п )

1) V 2; I п )

12и2 12иЗ

откуда следует, что ряд, общий член которого равен In J- , сходится.

Следовательно, сумма S первых п членов этого ряда имеет предел при п~оо. Эта сумма равна

5 ==1п(р( )-1п(р(1).

Поскольку последовательность 1пср( ) имеет конечный предел, то и последовательность f(n) также имеет конечный предел.

Мы уже знакомы (п. 2.1.4) с формулой Валлиса, которая имеет вид

2-Д 1.3...(2n-l).1.3...(2 +l)

JL- г 2 (пЦ

2 [(2/г)If (2/г+1)

Если заменить в этом выражении величину nl на основании формулы(1), то получим

откуда следует равенство

nl = ne~Ye .

где е стремится к нулю при п, стремящемся к бесконечности. Можно показать, что

1-2/г 3-4/j3 5.g/j6 7-8/г

Учитывая выпуклость кривой у~1пх, заключаем, что формула трапеций позволяет вычислить искомую площадь с недостатком, т. е.

п1п п - п > 1п /г! - Y In /г. Приближенно можно принять

пЫп - геяй1п/г! -

30 3- 42 -4- 30

(2/г)! 1

р = 1

На практике пользуются следующей приближенной асимптотической формулой Стирлинга:

nln e- Y (2)

или, если требуется большая точность.

Последняя формула делает ошибку пренебрежимо малой даже при малых значениях п.

Законы распределения случайных величин

9.1.5. Дискретные случайные величины. Пусть имеется некоторая группа событий

2 ..., Л,

вероятности осуществления которых равны соответственно

Pi р2.....Ps-

Условия опыта таковы, что в каждом опыте осуществляется одно и только одно событие (т. е. мы имеем полную группу несовместных событий). Поэтому

р1 + р2+ +Ps=-Рассмотрим переменную х, которая может принимать значения

в зависимости от происходящего события. Такая величина называется дискретной (прерывной) случайной величиной. Совокупность значений случайной величины вместе с их вероятностями определяет ее закон распределения.

Выражение

X = PiXi -Ь р2х2 + - + Pss = 2 PiXi (3)

называется математическим ожиданием случайной величины х *). Таким образом, математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений 1).

*) В советской литературе, помимо обозначения математического ожидания чертой сверху (как это принято в настоящей книге) применяется обозначение М [х], которое удобнее в случае, когда рассматривается математическое ожидание сложного выражения. Мы буде,м использовать, как правило, обозначение математического ожидания, принятое автором. Дисперсия случайной величины х обозначается D [х], или просто D.

) Если X - выигрыш в азартной игре, то игра может считаться справедливой, если математическое ожидание х равно ставке.

где fij, fig, fig, ...-числа Бернулли (п. 10.5.1):