наты, т. е. значению k, при котором достигается наибольшая величина Р {k). Известно, что это значение k тем ближе к пр, чем больше п. Так как нас интересуют главным образом большие значения п, то производим замену переменной:

k = np-{- X.

Новая переменная х представляет собрй отклонение

x=k - k.

При этом биномиальный закон распределения принимает вид

Pn(k = Jix)T(nci-y. P--V--- (26)

Вычисление P {k) по формуле (26) при больших х довольно неудобно. Кроме того, вероятность Р () дана здесь как функция трех параметров: k, п, р. Покажем, как можно получить более простую формулу, приближенно представляющую биномиальный закон распределения.

,9.1.12. Формула Лапласа. Нормальный закон распределения (закон Лапласа - Гаусса). Если использовать формулу Стирлинга для факториалов, то выражение (26) запишется в виде

\ пр

X \пр+х пр)

X \nq~x

/2.(;,+)(,-)/

Имеем [пр-

{nq-Отсюда

X) ln(l + - X) In ( 1 -

(пр + X)

2 пр ~ 3 и>з

= - {nq-x)

1 X

nq 2 nq 3 nq

Я () =

P-Q

2 npq 6 n- ff-q

y2m pq - -{p -

(27)

Формула (27) при сделанных допущениях позволяет приближенно найти вероятность того, что отклонение х имеет определенное значение (отличающееся от k на целое число). Эта формула не симметрична относительно х, что происходит из-за членов, содержащих х в нечетных степенях. Заметив, что все эти члены содержат множитель р - q, можно сделать вывод, что если р не слишком отличается от и если х не очень велико по сравнению с npq, то эта формула приближенно симметрична.

При больших п, если учитывать только члены первого порядка малости

- , формула (27) примет вид

е 2 ря-

относительно

Pnik)-

(28)

Y2inpq

Можно ввести в эту формулу математическое ожидание k~np или средйее Квадратическое отклонение a = Ynpq, в результате чего получаем две эквивалентные формулы:

Р (Д;) = --=е 2 . (29)

\2щк .

, X k - пр k-k

Величину \ - = у. = -называют приведенным или

относительным отклонением (она безразмерна). Величина h = =

V2npq

= называется мерой точности. Она по размерности обратна случайной

величине х

Придадим k или х, что одно и то же, два близких значения, отличающиеся на несколько единиц. Пусть эти два значения будут k, i- х. Разность между двумя соответствующими приведенными отклонениями и очень мала, если п велико. Ее можно без заметной ошибки принять за дифференциал:

dfi - h (ki - k2) = h (jCj - x.

Вероятность того, что случайное значение приведенного отклонения заключается между £ и E-f-J?, будет равна вероятности того, что значение k заключается между k и Иначе говоря,

p()dl=-e-K. (31)

Мы получили один из основных законов распределения, закон Лапласа- Гаусса, или нормальный закон, который представляет собой асимптотическую форму биномиального закона распределения для случая очень больших п, когда

j. k - пр

Примечательно, что нормальный закон распределения зависит только от относительной переменной

Вероятность того, что случайное значение k заключается между сильно отличающимися друг от друга значениями и 2 будет

f (32)

где Ej = A(i - пр), 2 =/2(2 - пр).

Биномиальный закон распределения, характеризуемый тремя параметрами, при помощи некоторых упрощающих допущений, к исследованию которых мы еще вернемся, заменен законом распределения с одной относительной переменной.

*) В работах зарубежных авторов вместо меры точности используется величина Т

величиной не пользуются.

и - - , которая называется единичным отклонением. В советской литературе этой

или \

Кривая у =3 L е~, называемая кривой Гаусса, изображена на рис. 9.6. У

Вероятность того, что приведенное отклонение заключается между двумя любыми значениями £j и равна площади криволинейной трапеции, заключенной между этой кривой, осью £ и двумя прямыми, параллельными оси Оу, пересекающими ось абсцисс в точках и Если разность - постоянна, то эта вероятность будет наибольшей в том случае, когда значения 5j и 2 равны по величине и противоположны по знаку.. Наибольшую вероятность имеет нулевое отклонение. Вероятность того, что приведенное отклонение примет любое значение, очевидно, равна единице. Но эта вероятность равна

Как известно (п. 7.3.1), данный интеграл - интеграл Пуассона - равен

Y l/ic; это хорошо согласуется со всем

изложенным выше.

Функция Лапласа (или интеграл вероятностей)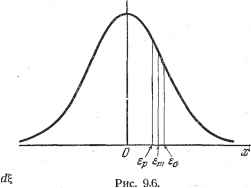

рассматривалась в и. 7.3.1 и- последующих, К приведенной там числовой таблице следует добавить следующие значения, играющие особую роль в теории вероятностей:

Если случайная величина представляет собой не приведенное отклонение f, а абсолютное отклонение х, то нормальный закон распределения принимает вид

р (х) dx -

{А2я

(33)

Так как нормальный закон распределения симметричен, то

F=o.

Среднее квадратическое отклонение в этом случае совпадает с корнем квадратным из момента второго порядка. Вычислим в общем виде момент