ВВЕДЕНИЕ

Предлагаемая работа не представляет собой курса математики в обычном смысле слова. В ней не следует искать связи между отдельными главами, кроме их общей направленности к применению в электро- и радиотехнике. Главная задача книги - представить в удобной и доступной форме те основные математические сведения, которые должен иметь инженер со средней подготовкой, чтобы с пользой для себя читать статьи и работы, в которых рассматриваются достижения науки в области слабых и сильных токов.

Для этой цели автор кое-где намеренно поступился строгостью доказательств в пользу краткости и ясности. Читатель, стремящийся к абсолютной математической строгости, должен будет обратиться к классическим трудам по анализу или к работам, цитируемым в ссылках.

Для того чтобы быть в курсе развития своей области техники, инженер должен следить за специальной литературой. Однако легко заметить, что это требует высокого уровня математических знаний. И если читатель будет вынужден, прежде чем приступить к чтению специальных работ, дополнительно изучать некоторые разделы математики, необходимые для понимания текста, то результат известен заранее: как бы ни была важна статья, она прочитана не будет; мало того, что это требует скучного труда, но в большинстве случаев необходимые сведения разбросаны по отдельным книгам и статьям, часто на иностранных языках, и собирать их долго и трудно.

Эту работу я и попытался проделать в данной книге. Особые старания были приложены к тому, чтобы читатель мог найти формулы, таблицы и кривые, необходимые для численных расчетов, которыми обычно завершаются инженерные исследования.

Эту книгу следует рассматривать, как некий рабочий инструмент.

Выражаю мою живейшую благодарность Луи де Бройлю, оказавшему мне честь представить эту работу читателю.

Обращаюсь с признательностью к Блан-Лапьеру, который соблаговолил взять на себя труд отредактировать часть IX главы, посвященной случайным функциям.

Андре Анго

ГЛАВА I

ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ

Рис. 1.1.

1.1. КОМПЛЕКСНЫЕ ВЕЛИЧИНЫ

1Л Л.Определения. Вещественное число можно изобразить графически. В самом деле, пусть хх (рис. 1. 1) - бесконечная прямая, на которой выбрано положительное направление. От точ-- . ки О, принятой за начало, отложим в опре-

деленном масштабе отрезок, длина которого пропорциональна рассматриваемому вещественному числу. На рис. 1.1 отрезок OA представляет положительное число, а ОВ - отрицательное. На прямой хх размещаются все вещественные числа: целые, дробные, алгебраические, трансцендентные, причем как положительные, так и отрицательные.

Понятие вещественного числа можно обобщить, если ввести в рассмотрение число Z, образованное парой вещественных чисел х и у, взятых в определенном порядке. Такое число назовем комплексным. Временно будем записывать его в виде

Вещественные числа х и у составляют соответственно вещественную и мнимую части комплексного числа z. Часто используются обозначения

x = R(2), У=1(г).

Комплексные числа также можно изобразить графически. Это изображение будет двухмерным на плоскости, образованной двумя взаимно пер- . Рис. 1.2. пендикулярными осями Ох и Оу.

Комплексное число на плоскости хОу (рис. 1.2) представляется точкой М с координатами х, у; эту точку называют также изображением комплексного числа. И обратно, пару чисел \х, у\, образующих комплексное число z, называют аффиксом точки М.

Два комплексных числа z = [х, у\ и z - \х, у\ считаются равными, если совпадают изображающие их точки. Это означает, что равенство z w. z имеет место в том, и только в том случае, когда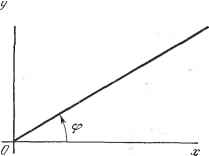

Если изображение комплексного числа совпадает с началом координат, то его вещественная и мнимая части равны нулю. Такое комплексное число называют нулем. Следовательно, равенства z = 0 к х - 0, у- О равносильны.

Положительное число р - }/х-\- у, равное длине отрезка ОМ (рис. 1.2), называется модулем комплексного числа z; модуль z обычно обозначают z . Угол ср, на который нужно повернуть ось Ох в положительном направлении (против часовой стрелки) до совпадения с направлением ОМ, называется аргументом комплексного числа z. Этот угол определяется с точностью до целого числа оборотов; углы ср--2/%1г также будут представлять собой аргументы Z {k может принимать все возможные целые значения: положительные, отрицательные и нуль).

Если заменить х на рсозф, а у на psincp, то комплексное число можно написать в таком виде:

2 = [pcoscp, psin9].

Вместо того чтобы изображать комплексное число [х, у] точкой М, мы можем представить его отрезком ОМ. И обратно, отрезок ОМ изображает комплексное число [х, у].

1.1.2. Сложение. Суммой двух комплексных чисел z и 2 называется комплексное число z, вещественная и мнимая части которого представляют собой соответственно сумму вещественных и мнимых частей z и

Z=[X, y] = 2i+22 = [Xi + X2, yi + ygl-

Пусть точки М, М2 и М - изображения чисел z, Z2 и z: Из рис. 1.3 видно, что точка М может быть получена по точкам Ж1 и Ж2 с помощью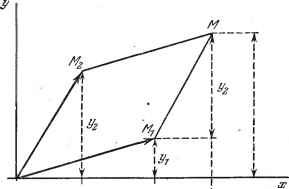

:----------*-1

Рис. 1.3.

правила параллелограмма. Следовательно, сложение комплексных чисел z- и 2 графически представляется как геометрическое суммирование отрезков ОМ и ОЖ2.

Если р, и р2 обозначают модули Zy и z-. то из рис 1.3 непосредственно следует справедливость двух неравенств:

I21+22KP1 + P2. Ii -22>р, -P2I.

1.1.3. Умножение. Пусть z - \x,y, 2Г2 = [Х2, У2] - -ва комплексных числа, изображения которых суть точки М- и М. Произведением этих двух