ТОК /. Каждый электрон создает импульс, который вызывает некоторое возмущение в усилителе, и электрические явления, которые в нем происходят, подобны в совокупности движению маятника, возбуждаемого последовательными толчками. Не уточняя пока, скажем только, что усилитель подвергается ряду одинаковых очень коротких и беспорядочных ударов. Каждый из них соответствует импульсу, создаваемому одним электронным зарядом е;

среднее число импульсов в секунду будет равно = у. Действие тока /

будет совершенно определено, если будет известна бесконечная последовательность моментов времени

.... tj. .....

в которые действуют отдельные электроны. Мы можем охарактеризовать линейный усилитель реакцией /? (t), которая соответствует очень короткому единичному импульсу (т. е. очень быстрому прохождению единичного заряда), полученному в момент времени = 0. Реакция R{t) называется ударным ответом усилителя (рис. 9.8). Очевидно, что ответ /?(> тождественно равен нулю при f < О, так как следствие не может предшествовать причине-Ответ на импульс, полученный в момент tj, очевидно, равен eR(t - tj) и в конечном счете x{t) представляется как наложение в момент i ответов усилителя на все удары, предшество-Рис. 9.8. вавшие моменту t. Можно, впрочем, распро-

странить суммирование на все удары как предшествующие, так и следующие за t, так как последующие удары все равно исключаются сами собой как следствие условия R(t - tj)=0 при t<tj. Поэтому

R(t)

x(t) S eR{t - tj)= 2 eR{t~tj). (52)

tj<t ij>-co

В этом примере случайность входит через свойства последовательностей

----ij tj+V tj+2 -

Существует столько же возможных случайных реализаций функции x{t), сколько имеется таких последовательностей.

Так же, как и ранее. Можно считать, что влияние случайности проявляется в бесконечной последовательности элементарных испытаний, в каждой из которых случайным образом определяется момент tj Y, если все моменты tj, tj y, tj 2 известны). Можно также назвать испытанием совокупность всех значений частного распределения tj от t- - оо до t - -\-co.

В рассмотренных до сих пор примерах мы прежде всего выясняли схему случайной природы явления, порождающей случайную функцию. Категория испытаний могла при этом быть более или менее сложной, но она была вполне определенной. При различных применениях теории вероятностей

) Эта точка зрения устанавливает четкое различие между прошедшими опытами, результаты которых известны в момент t, и будущими опытами, сохраняющими еще все случайные возможности.

довольно часто употребляется понятие случайной функции при менее ясных на первый взгляд обстоятельствах. Возьмем пример: известно, что под влиянием перемещений масс на поверхности Земли, о которых еще нет достаточных сведений, полюс Земли претерпевает небольшие перемещения. Значения координат ATj и yj полюса, выраженные в большинстве случаев в секундах дуги, определяются по отношению к системе прямоугольных осей, за начало которых принимается среднее положение полюса, а ось Xj проходит через Гринвичский меридиан. Рассмотрим, например, координатуХ,. Ее изменения во времени за последние десятилетия представлены кривой, ход которой дан на рис. 9.9. Ход этой кривой достаточно незакономерен, чтобы навести на мысль о случайном характере явления, однако на первый

Рис. 9.9.

взгляд всякий вопрос о вероятности из этой задачи исключен. Значения Xj() нам становятся известны лишь по мере того, как производятся с течением времени наблюдения. Конечно, мы не знаем будущего функции Xj(), но эта функция единственна, так как во Вселенной имеется всего одна Земля. Однако если имеется некоторая теория о природе масс, случайные перемещения которых порождают изменения в положении полюса, или если нами приняты достаточно точные гипотезы об этих массах и их перемещениях, то нам ничто не мешает мысленно рассматривать бесконечное количество систем, макроскопически тождественных Земле и отличающихся друг от друга только случайным различием поверхностных масс, перемещения которых мы подчиним некоторым случайным схемам. При этом мы должны будем считать, что наблюдаемая функция xt) представляет собой лишь возможную реализацию случайной функции х (t), определенной по категории испытаний, имеющей, так сказать, только мысленное существование. Такой способ рассуждений законен лишь в том случае, если у нас есть причины считать, что мы сможем, исходя из статистических свойств случайной функции х(), определенной по воображаемой категории испытаний, вывести результаты, справедливые для дальнейшего хода частной реализации функции х() и, в частности, для лгД). Тогда мы сможем увидеть, приводят ли принятые гипотезы к результатам, которые подтверждаются опытом, и в благоприятных случаях сможем предвидеть в известной мере будущее функции Xi(t). По аналогии с уже рассмотренными примерами можно сказать, что скорость ветра или температура воздуха - случайные функции времени в некоторой определенной точке Земного шара.

9.2.2. Функции распределения. Изучение случайной величины показало, что не всегда нужно полностью знать схему случайности и что если известна функция распределения случайной величины, то с вероятностной точки зрения поведение этой переменной, взятой изолированно, также будет- определено. Что можно сделать при аналогии применительно к случайной функции x(t)?

Прежде всего рассмотрим фиксированное значение t,. При этом x(tj) есть случайная величина и естественно будет ввести ее функцию распреде-лония. Обозначим эту функцию Fx; t,), имея в виду, что F представляет

собой вероятность осуществления события < atj. Очевидно, что момент не имеет никаких преимуществ перед другими, и, следовательно, мы приходим к постановке того же вопроса для всех моментов t, иными словами, пытаемся найти функцию распределения F (х; t) для всех моментов t. Зная F{x; t), мы будем знать в каждый момент времени распределение наблюдаемых значений. Этого, однако, недостаточно, чтобы получить полное представление о поведении функции х (t) и, в частности, чтобы определить ее развитие во времени, что ясно видно на следующем примере. Пусть <р - случайная величина, которая с равной вероятностью может принимать все значения в интервале [О, 2тс]. Каждому значению (р соответствует функция х (t) = siu{wtгде (d - известная постоянная. Таким образом, определена случайная функция по категории испытаний, соответствующей всем возможным значениям <р. Можно без труда получить функцию F (х; t). Она не зависит от t и отвечает плотности вероятности , - dF 1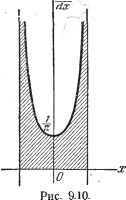

(53)

представленной на рис. 9.10).

Введем теперь еще одну случайную функцию y(t), определенную по той же категории испытаний, что и раньше, и рассмотрим для любого значения <р следующую функцию, постоянную при всех t:

у () = sin ср.

Функция распределения F (у; t), соответствующая y{t), тождественна функции F{x; t), соответствующей л: (О. однако обе случайные функции x(t) и y(t) имеют очень мало сходства. В частности, каждая реализация x{t) представляет-собой синусоиду, тогда как каждая реализация y(t) - прямая, параллельная оси времен. На рис. 9.11 приведены кривые, представляющие функции X (t) и у (t) для некоторого значения ср (be = sincp).

Этот простой пример показывает, что недостаточно знать F (х; t), чтобы

охарактеризовать цепь значений, которые последовательно принимает х с течением времени. Другими словами, знание функции F(x, t) не дает связи между различными случайными значениями, которые принимает x{t) в различные моменты времени. Мы вынуждены поставить вопрос: если и 2 - -ва любых частных значения, то каковы должны быть статистические свойства совокупности двух случайных величин х (t и х (ti (Речь идет

Рис. 9.11.

) Вероятность того, что значение х {t заключается между х, и х, -- Дх равна вероятности того, что значение ip заключается между arcsin х, - со и arcsin (х, +- Дх) - со. Вследствие того, что случайная величина у равномерно распределена между О и 2я, вероятность Д/ равна

~ [arcsin (х, -1- Дх,) -arcsin х,].

Отсюда находим

Д Дх,

а в пределе

dF dx

при X = Xi.