Ф(И1, 2. ; 2. .... )=-e-f . (.)+-+V( )]. . (54)

Прежде чем покончить с вопросом о функции распределения, сделаем еще три замечания. !-

1. Можно попытаться приближенно описать поведение функции x(f), пользуясь ограниченным числом особенно типичных значений. Для этого следует ввести моменты или средние значения ). Это обстоятельство не является новым при изучении случайных величин, но новым оказывается весьма большое количество рассматриваемых моментов, что объясняется введением переменного параметра t. Следует ввести:

а) момент первого порядка x(t), представляющий собой функцию одной переменной t;

б) наиболее общий момент второго порядка - математическое ожидание произведения х (t) х {t,, представляющее собой функцию двух переменных 1 и В частном случае, когда = f2 = t, мы снова получаем начальный момент второго порядка x{t), зависящий только от одной переменной /;

) Термин среднее значение здесь употребляется в смысле математического ожидания. Когда речь пойдет о средних по отношению к времени или к любому другому параметру, это будет специально оговорено.

в большинстве случаев о случайных величинах, связанных между собой вследствие наличия некоторой непрерывности явлений во времени.) Мы узнаем статистические свойства двух связанных между собой величин x{t и xit), если нам станет известна функция распределения Fx х, t t, соответствующая совокупности этих двух случайных величин.

Напоминаем, что функция F {х х, t 2) представляет собой вероятность одновременного осуществления неравенств:

a:(ji)<Xi и xitXx.

В общем случае мы получим представление о статистических свойствах случайной функции x{t), если сможем ответить на следующий вопрос. Пусть j, 2> scTb п значений t (п - любое, но конечное число), выбранных любым способом. Какова функция распределения F(х х. .., х; t 2.....in) соответствующая совокупности связанных между собой случайных переменных х {t{), х {t), .. ., х (/ )? Вследствие изложенного мы заключаем, что случайная функция определена, если известна функция распределения F, соответствующая наиболее общему случаю. Известную функцию распределения F (atj, Х2.....л: ; t t, - . ., ) можно заменить соответствующей характеристической функцией, определенной по совокупности связанных между собой случайных величин х (t,), х (t), . . ., х (i). Напоминаем, что если X Х2, .... х есть п случайных величин, определенных по одной и той же категории испытаний, то характеристическая функция, отвечающая этим п переменным, является математическим-ожиданием величины е-[ г1 2-2+ + 1], которое представляет собой функцию п переменных Mj, Й2, .... к . В рассматриваемом случае характеристическая функция,

соответствующая функции распределения F, будет равна е-[ i-Ci)* VCMl для заданных значений t 2. - -. tn- функция п переменных j, 2, . .., гг , которая зависит от п параметров -/г моментов времени t ?2> п- Следовательно, характеристическая функция, соответствующая функции распределения F, - это функция Ф от 2/г переменных и U2.....к ; t 2> п-

Она определяется формулой

в) наиболее общий момент порядка п - математическое ожидание произведения X (i) X (2) X (t ), представляющее собой функцию п переменных. Он включает все частные случаи, которые можно получить, связывая между собой значения t, в частности момент x {t), который получится при условия, что все значения t одинаковы.

Совершенно очевидно, что все эти моменты можно получить, зная F{Xi, х, .... х ; t, 2. in)- Еще удобнее получить их, если известно

разложение в ряд в окрестности начала координат для характеристической функции ,

Ф(М1, 2, и ; 2.....*п)-

Известно (п. 9.1.8), что знание характеристической функции позволяет получить моменты любого порядка. Мы применяли это, в частности, для случая совокупности двух связанных между собой случайных величин (формулы (19)).

2. Чтобы уточнить связь явлений во времени, естественно поставить вопрос, в какой мере знание значений Xj, Х2, х, полученных для x{t) в моменты j, t, tj, может определить значения xJ, х, .... xJ, отвечающие моментам t[, t.....t. Иными словами, речь идет о знании условной вероятности для / величин х (j), х t, ..., х в предположении,

что значения х (j), х (2).....х {t известны. Эта условная вероятность

описывается функцией распределения, которую мы обозначим F(х, х, ...

tj. Она представляет собой

вероятность одновременного выполнения неравенств

х(;)<х;; х()<х;; х(;)<х; в предположении, что справедливы k соотношений

X (i) = Хр X (2) = Х2, X (t = Xj.

функции условного распределения, которые только что были введены, получаются из априорных функций распределения (т. е. определенных при отсутствии каких бы то ни было дополнительных условий) F (Xj, Xg, ..., х; j, 2 tk) путем применения теоремы умножения вероятностей. Пример

этого приводится ниже. В на- стоящий момент ограничимся по-

казом на конкретном случае важности изучения условных вероятностей.

Допустим, что мы наблюдаем явление x(f), имеющее случайный характер, определенное по известной категории испытаний S. Рассмотрим определенный опыт, приводящий к явлению X, и отметим значения х в моменты ®, 1, 2, 3, k. Отложим на графике (рис. 9.12) соответствующие точки (t, х). Пусть это будут Яц, Pj, Р.. Если явление х

развивается достаточно медленно, то мы можем соединить точки непрерывной кривой, которая представит с.хорошим приближением ход изменениях (О в интервале О < t k. Положим теперь, что наша информация не превышает момента tj. Значения функции х (t) для моментов, будущих по отношению к моменту tf, являются случайными. Если бы мы все же захотели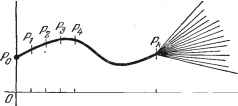

12 3 4

Рис. 9.12.

произвести экстраполяцию, то, предполагая некоторую непрерывность явления, могли бы в течение, некоторого, не слишком большого отрезка времени продолжить кривую как ее касательную в точке Р,. Однако чем больше мы станем продвигаться в будущее, тем меньше будет обоснована такая экстркполяция. Строго говоря, начиная с момента t, совокупность возможных реализаций неограниченно расширяется, и становится возможным бесконечное количество кривых, как это показано на рис. 9.12. Некоторые из этих возможных кривых имеют больше шансов быть наблюденными, чем другие. Поэтому представляет интерес изучение случайных величин x(t,

x(t.....x{t, когда x(l), х(2).....x{k) имеют значения, полученные

в предыдущем опыте (значения t, t, ..., t все больше ky

3. Приведенные до сих пор примеры относились к случайным функциям времени. Это особое значение, придаваемое параметру t, дает возможность сделать изложение более наглядным, но следует иметь в виду, что f не обязательно должно представлять собой время и может быть любым параметром. Можно, например, сказать, что в некоторый момент скорость турбулентной жидкости является случайной функцией координат.

Проблема сходимости

9.2.3. Введение. Прежде чем покончить с вопросом об общих понятиях, мы должны сказать несколько слов о новом аспекте, который получает столь существенное в анализе понятие сходимостипри замене определенных величин случайными величинами. В анализе принято говорить, что величина f (t) - функция параметра t - стремится к при t, стремящемся к о> сли по любому сколь угодно малому наперед заданному числу е > О можно найти такое число tj > О, что выполнение неравенства \t - t] <Cf} влечет за собой выполнение неравенства / - /ol<s-

Рассмотрим теперь случайную переменную х (t), зависящую от параметра t (иначе говоря, случайную функцию), определенную по категории испытаний . Когда можно сказать, что при t, стремящемся к t, x(t) стремится к некоторому пределу? Очевидно, что предел этот не может быть ни чем иным, как только случайной величиной, которую мы назовем jcg (в частном случае случайная величина Xq может оказаться определенным числом). Говоря, что случайная переменная х (t) стремится к случайной величине Xq, мы имеем в виду, что x(t) все меньше и меньше отличается т Xq. Но если в анализе это имеет тот однозначный смысл, что / - fg\ становится все меньше и меньше, то гораздо труднее определить, что именно имеется в виду, когда говорят, что одна случайная величина мало отличается от другой. Как мы увидим ниже, это выражение можно истолковывать различными способами, откуда следуют и различные определения понятия сходимости. Сделаем несколько замечаний.

9.2.4. Сходимость в смысле Бернулли. Говорят, что случайная функция X (t) стремится к Xq в смысле Бернулли, если функция распределения F {х; t), относящаяся к x{t), стремится (равномерно в любом конечном интервале) к функции распределения случайной величины Xq. Такое определение сходимости крайне неопределенно. Действительно, вернемся к обоим примерам случайных функций, которые бьши рассмотрены в п. 9.2.2. Обозначим через F (х; t) и F (у; f) соответствующие функции распределения. Мы уже знаем, что они тождественны и не зависят от времени. Поэтому x{f) сходится к у(о) Е смысле Бернулли, если t стремится к t. Что же происходит в действительности? Для большей наглядности положим Iq-. Тогда