неравенством Буняковского-Шварца*). Пусть даны две случайные величины X и К, независимые или зависимые. Кроме того, дано вещественное положительное или отрицательное число L Тогда справедливо очевидное неравенство (TZ+l0>0, откуда

Это должно иметь место при любом X, следовательно, квадратное уравнение Xl?-\-2XY\-\-Y = 0 не должно иметь различных вещественных корней. Поэтому

<2-F2. (72)

Это и есть неравенство Буняковского - Шварца для рассматриваемого случая. Применим его к двум случайным величинам x{t) и x(t-i), которые являются значениями случайной функции x{t) в моменты t к t Имеем

\х (t)xit - ) р < t) -xt - -с).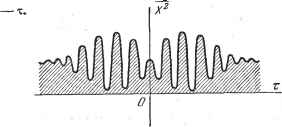

Рис. 9:15.

функцию применительно к явлению

Взяв квадратный корень, получаем требуемое неравенство (71):

р()<Р(0).

Согласно соотнощению(71), модуль корреляционной функции достигает наибольщего значения при z - O. Если рассматривать корреляционную

интерференции, то неравенство (71) означает, что наибольшая интенсивность, если речь идет о системе интерференции с блестящей средней полосой (или наименьшая интенсивность, если речь идет о системе с темной средней полосой), всегда бывает в средней полосе. В частности, таких полос, какие изображены на рис. 9.15, наблюдать нельзя.

9.2.11. Непрерывность. Дифференцируемость. Выясним, при каких условиях функция x(t) будет непрерывна по в среднем квадратическом. Непрерывность в среднем квадратическом существует, если л:(--ДО сходится к x(t) в среднем квадратическом при At, стремящемся к нулю, иными словами, если справедливо равенство

(73)

lim {x{t+ At) - x{t)\==:Q.

Необходимым и достаточным условием непрерывности случайной функции х {t) в среднем квадратическом, является непрерывность корреляционной функции Е начале координат. В дальнейшем будем предполагать, что это условие выполняется. При этом можно показать, что корреляционная функция будет равномерно непрерывна при -оо<т<--оо.

Совершенно очевидно, что локальные свойства x(t) связаны с поведением p(i) при малых значениях z. Мы только что видели, что непрерывность x(t) в среднем квадратическом зависит от непрерывности р(х) в начале координат. Исходя из этого, можно теперь сформулировать следующую

) Неравенство Буняковского - Шварца имеет вид

6 12 6 6

jf{x)g{x)dx <jf4x)dx.jg2(x)dx.

,- x{t-\-Lf) - x{t)

л:<2>() = 11тс. к.

х ) {t + t) - x> (О At

(74)

, . ,. x< -У{t-{-At)~x< -){t) л:< >()== hm С. к. -J-!---

Прежде чем идти дальше, необходимо указать на одно свойство сходимости в среднем квадратическом.

Если две случайные величины X (а) к Y (а), зависящие от параметра а, сходятся в среднем квадратическом соответственно к Xq и Kq при а, стремящемся к ttfl, то X (а) К (а) стремится к XqYq )

Если в частном случае X не изменяется вместе с а, то

nmXY{a) = XYQ. Применим этот результат к случайным величинам

Имеем

iL(+Jbz.x( ,) tp(, Д0 р(,)]. (75)

Имеем

) Действительно, положим

x(a) = X(a) -Хо; У(а) = К(а) -Ко.

lim х2 (а) = 0; lim у (а) = 0.

С другой стороны.

X (а) Y (а) = \Хо + Х (а)] [Кр -f у (а)] = ЛГоКр + X (а) У + У (а) Х + X {а) у (а).

Из неравенства [Иварца следует, что

U WToT< У)У1: >()оК V7V)l: \х{а)у(а)\ VT)), откуда

Jim Х(о.) К (а) = ХоГо-

5 a-XZj

теорему: Для того чтобы стационарная случайная функция второго порядка х {€) имела -Ю производную в среднем квадратическом, необходимо и достаточно, чтобы при т = О существовали все производные корреляционной функции р (т) до 2 -го порядка включительно.

Если обратиться к рис. 9.14, то ясно, что корреляционная функция, изображенная сплошной линией, соответствует случайной функции, не имеющей производной в среднем квадратическом. Действительно, производная р(0) не определена. Напротив, корреляционная функция, которая вблизи точки т = 0 идет по пунктирной кривой, соответствует случайной функции, имеющей производную в среднем квадратическом. Предположим, например, что

dp if о ,

производные , .....существуют при т = О (тогда можно показать, что они существуют при любом т). Из этого следует, что случайные

dx dx dx

производные , , существуют. Для простоты записи обозначим их через х-> (t), x-t), .... Напоминаем, что они определяются соотношениями

Устремим Дг к нулю: х (t - т) не изменяется, а величина -----~

стремится в среднем квадратическом к л:* (t). Следовательно, левая часть равенства (75) стремится к i> (t) х (t - т); взяв предел правой части, получаем

x4t)x(t-z)=. (76)

Таким же образом можно найти

x(t) х(1>( -т) = -

(77)

Мы свели в табл. I выражения типа (77). Они выражают то, что можно назвать смешанными корреляционными связями между х (t) и ее производными. В верхней строке и в левом столбце этой таблицы помещены величины, служащие сомножителями:

X (t). х<1> (0. х(2) (t), ....

Х( -Т), Xt - Z). х(2)( -Т), ...

Из табл. I можно определить значения математического ожидания произведения двух величин, помещенных в заголовках соответствующих строки и

Таблица I

столбца. Если приравнять z==0. то, принимая во внимание, что производные нечетного порядка равны нулю при т = 0. получим результаты, приведенные в табл. II.

Полезно напомнить, что значения, принимаемые в определенный момент случайной функцией и ее производной в среднем квадратическом, не коррелируют:

J(t)x(t) = 0. (78)

Мы приводим здесь снова замечание, которое было уже сделано, когда речь шла о различных видах сходимости последовательностей случайных величин. Производные, которые мы сейчас рассматривали. - это производные