Если Z пробегает вещественную ось от - оо до А, то точка z описывает вещественную ось от точки с абсциссой т, соответствующей X - -со, до точки с абсциссой а, соответствующей Х-А (рис. 1.50), -это имеет

Ллосггость т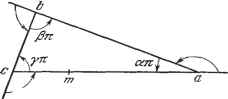

-тс (у-7)

77лос/<ость Z

-7т:(а:-7)

Рис. 1.50.

место, если выбрать ту ветвь / (г;),. определяемую формулой (17), для которой аргумент / (Z) при - со < А < Л равен нулю. Возможность такого выбора обеспечивается равенством (18). Имеем

а=т-\- f f{X)dX.

При переходе точки X через А соответствующая ей точка плоскости Z переходит с вещественной оси на прямую, составляющую с этой осью угол -л (а-1). По новой прямой точка z движется до точки -Ь, которая соответствует точке Х - В вещественной оси плоскости Z, причем

Ь=а + е}---> f f{X)dX.

При переходе точки X через В соответствующая ей точка плоскости z снова переходит на другую прямую, составляющую с предыдущей угол - it(p-1). По новой прямой точка z доходит до точки с, которая соответствует точке Х - С вещественной оси плоскости Z, причем

с = й--е-/(Р- ) f f(X)dX.

Наконец, при переходе X через точку С соответствующая прямая в плоскости z поворачивается на угол -1(7-1), и при Л->-оо течка z стремится к начальной точке т, оставаясь на этой прямой. Имеем

те=гс + е-/(г-1 J f{X)dX.

В силу соотношения (18) отрезки ст. и та являются продолжением один другого.

Таким образом, каковы бы ни были числа А, В, С, функция (17) определяет отображение, которое преобразует треугольник, подобный данному, в вещественную ось У-О. Для перехода к заданному треугольнику достаточно

1.4] КОНФОРМНЫЕ ОТОБРАЖЕНИЯ 81

В интеграле (17) ввести постоянный множитель, учитывающий отношение сходственных сторон треугольника.

Многоугольник, рассматриваемый в отображении Шварца, всегда может быть построен по заданным условиям; он может иметь вершины в бесконечности.

Пример 2. Рассмотрим две параллельные прямые, одна из которых разорвана (рис. 1.51). Эту фигуру можно считать многоугольником. Вершина а находится в бесконечности, сторона аЬ сливается со стороной be.

j-tz

ах.

Рис. 1.51.

Вершины с к d находятся в бесконечности. Сторона de сливается со стороной ef, и многоугольник замыкается прямой на бесконечности. Величины углов it(aj-1), Jt(a2-1), ... обозначены на рисунке.

Следовательно, функция, определяющая преобразование, имеет вид

/(Z-B)(Z-£) .} {Z - C)(Z~D)

Из четырех вещественных чисел В, С, D, Е три можно выбрать произвольно. Учитывая, что В <С С <С D <С Е, можно положить В - - 1, £ = -1- 1, С = - d, Dd(0 <d < 1). Тогда z

Г - 1 . , d - l , Z - d , .

Определим постоянную так, чтобы начало координат плоскости z отображалось в начало координат плоскости Z. Имеем

. 1 - const == yir -,

т. е. искомое отображение принимает вид

, О - Х , Z - d , \ - d , = --d-i z + d--Sd--

Отделяя вещественные и мнимые части, найдем соотношение

, . d - \ , 2dY , l-d . .

-l-y-arctg--ру,---2d~J

из него непосредственно получаются параметрические уравнения кривых, отображениями которых служат прямые X = const а Y - const, параллельные осям координат плоскости Z. Покажем, что при перемещении точки Z по оси У -О точка z описывает рассматриваемую фигуру в плоскости z. Если X находится вне интервала (-d, d), то

, d - \ , X - d = -i--2d- -X+d- .

1-d2

xjyX + jy + \n

Если X находится внутри интервала (- d, d), то под знаком логарифма стоит отрицательное число, аргумент которого равен vi соответственно

находим

х = X -\--- In

2d d + X \~d

Используя полученные формулы, заполним таблицу, описывающую изменения на плоскости z при пробегании X вдоль вещественной оси плоскости Z (рис. 1.52):

Для полного совпадения полученной и заданной фигур достаточно, чтобы отнощение

расстояние be

расстояние между прямыми

для обеих фигур было бы равным. Из этого равенства определяется число d.

Только что описанное отображение позволяет рещать задачи плоского поля, в которых фигурируют две параллельные плоскости, причем одна из

А У-

В -t-

-со -/ d */

Рис. 1.52.

-СХ)

них рассечена бесконечной трещиной. Найдем, например, силовые и эквипотенциальные линии электростатического поля, возбужденного бесконечной плоскостью и двумя полуплоскостями, имеющими потенциал V.

. Эквипотенциальные и силовые линии являются соответственно отображениями прямых Y = const ш X - const. Отметим, что такие же линии возникают в электростатическом поле, созданном бесконечной плоскостью, пересекающей плоскость Z по прямой К=0.

Рассмотрим ту же задачу для случая, когда на бесконечной плоскости и на двух полуплоскостях созданы разные потенциалы. Эта задача сведется к задаче для полосы щириной в 2d в плоскости Z, окаймленной двумя бесконечными полуплоскостями, причем полоса и полуплоскости обладают разными потенциалами. Легко заметить, что рещение задачи дается с помощью отображения ж) п. 1.4.2. Действительно, при рассмотрении плоскости комплексной переменной С видно, что

, , Z~d