= х2(;) = а2 = р(0);

Поэтому

Aj = = (0 (tj) = Р (, - t,). Q(u и, Ui,)= 2 Р(ti - ij)-iij

i = l, 2, ft y=l, 2, ft

ф( и ..., ,)=г2М)ч

(112)

(113)

Если нам нужно, снова перейти к закону распределения, то достаточно

вспомнить, что плотность вероятности Pix х.....х) представляет собой

коэффициент преобразования Фурье для характеристической функции Ф(Ир Kg, ...,и), как это следует из определяющего соотношения

ф = ( ..+ --Vfe)= J J J ... J( ..+ -+Vfe)pxi ... dx. (114)

В общем случае, если через jQ обозначить главный определитель квадратичной формы <5, а через <5 - обратнзЮ квадратичную форму, то

(1. 2.....47iW

(27.) 2

Напомним, что если коэффициенты квадратичной формы Q образуют квадратную матрицу [Л,-,-], то коэффициенты обратной квадратичной

формы <5 образуют квадратную матрицу \Ац\, где Aij = j~, а ац - алгебраическое дополнение элемента Ац в определителе Q.

Основное следствие предыдущих соотношений заключается в том, что закон распределения, которому подчиняются k случайных величин х х, .... х всегда можно полностью определить, если известна корреляционная функция!

Корреляционная функция, которая в общем случае имеет только энергетическое значение, определяет теперь все статистические свойства случайной функции x{t). Именно потому, что многие случайные процессы, изучаемые в приложениях, описываются стационарными случайными функциями Лаплвса- Гаусса, корреляционные функции играют такую важную роль. В частности.

ных величин х (t{), x(t,.....x{tj) подчиняются нормальному закону распределения для к случайных величин. Такие законы представляют собой обобщения нормального закона распределения, относящегося к одной случайной величине. Проще всего определить их, обобщая соотнощение (109), Можно сказать, что характеристическая функция нормального закона распределения для k случайных величин - это функция ф (Kj, ..., и). определяемая соотнощением типа

ф( 1, 2, .... ,) = . > =Ч . (110)

где <Э - неотрицательная квадратичная форма:

<3(Ki. %.....и)= 2 AijUUf. (Ill)

/=1, 2, к j=l,2....,k

Коэффициенты Ац имею1; очень простой смысл. Мы уже видели, что коэффициенты разложения функции ф в ряд вблизи точки Kj = = - - непосредственно связаны с моментами. Следовательно, можем написать

jc+iO; x2?=g2?1 . а ... (2-1), (116)

где 9 -целое положительное число. Ь) k = 2.

Рассматриваются две случайные функции x(t{) и x{t. Положим, что 6 = 1 - 2- Тогда

Ф( . 2) = { ° . (117)

причем очевидно, что

а2 = р(0).

Соответствующая плотность вероятности равна

1 р(0)[л: + л]-2рге1л-,д:2

2и Ар2 (0) - р2 (ly

Сделаем несколько выводов из соотношений (117) и (118).

9.2.16, Связь явлений во времени. Возьмем фиксированное значение Ху и найдем условную плотность вероятности P(x,Xi) значения Х2, если известно Xj. Вероятность /(х X2)<Xi<X2 получения в моменты и значений х, и х (с точностью до dx и dx, равна, согласно правилу умножения вероятностей, произведению вероятности P(x{)dxy иметь в момент значение Xj (с точностью до £?Xj) на вероятность Pixjxdx иметь в момент 2 значение Х2 (с точностью до dx<, если известно, что в момент получено значение Xj (с точностью до dx-. Поэтому

P(X2/x0rfX2 = %g. . (119)

Отсюда, используя предыдущие результаты, получаем

2 02(6)

1 1 Р(0)--

P(Xo/Xi)rfXo=--L.--- 3-е р№ dxn. (120)

/<°-

Это снова закон нормального распределения. Математическое ожидание дается формулой

2=f-s = Pi. (121)

а среднее квадратическое отклонение равно

<.)-~Щ--УрУУ--- (122)

Если 6 меняется от О до оо. то fi меняется от 1 до 0.

шумовой фон в линейных усилителях приводит во всех случаях к режимам, описываемым стационарными случайными функциями Лапласа - Гаусса.

Уточним предыдущие выводы, рассмотрев два частных случая А = 1 и k = 2.

а) А=1.

Мы уже получили выражения для характеристической функции и плотности вероятности. Разложение характеристической функции в ряд дает сразу же значение всех моментов. Как известно из. п. 9.1.13,

На рис. 9.21 представлено изменение математического ожидания jC9 = pXj (/) и значений, отстоящих от него на одно среднее квадратическое отклонение в каждую сторону (2).

Рис. 9.21 дает очень точное представление о том, что можно назвать непрерывностью явления во времени или еще статистической памятью функции x(:t). так как он показывает, каким образом знание значения влияет на возможность получения значения Х2. Можно заметить, что эта непрерывность явления во времени находится в прямой и исключительной зависимости от корреляционной функции, чем и оправдывается ее название; при этом не следует упускать из виду, что все сказанное справедливо только для стационарной случайной функции Лапласа-Гаусса.

9.2.17. Флуктуации в нелинейных системах. Обратимся снова к схеме на рис. 9.19. Мы уже видели, что изучение флуктуации после выпрямления требует зна-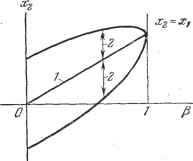

Рис. 9.21. функции Лапласа - Гаусса, то

ния корреляционной функции У {t) у {t - z). Если речь идет о стационарной случайной вычисление этой корреляционной функции несложно во многих случаях, т. е. для довольно многочисленных вариантов характеристик выпрямителей. Приведем несколько примеров.

/) Квадратичный выпрямитель {характеристика у = х). Математическое ожидание для выпрямленного тока разно

у = ]==р(0). (123)

Вычислим корреляционную функцию, ~y{t) - у (О- Имеем

относящуюся к отклонению V{t)=

Y{t)V(t - x)=r= [х2 (О - ХЦ [Х2 (t - z) - Х] = Х2 (О Х2 {t - z) ~ {xf.

Момент четвертого порядка получается из разложения в ряд характеристической функции Ф{и %) для функщ1Й x{t и х {t при ti=t и t2~t-z. Применяя уже указанный метод, находим

x\t)x{t - z) == 2р2 (т) -f р2 (0). (124)

Отсюда

Y{t)Y{t~z) 2р2 {Z). (125)

Таким образом, корреляционная функция на выходе квадратичного выпрямителя равна удвоенному квадрату корреляционной функции на входе.

Аналогичные расчеты позволяют рассматривать случаи характеристик более сложного вида, в частности, характеристики у = х {р - целое) или y=:fl-f ajX-t-CjX-f ...

Вычисление моментов второго порядка V() Y{t-z)=.{y{t)-y){y{t-z)-у) сводится к вычислению моментов, которые получаются на основании разложения в ряд характеристической функции Ф(К, и.

2) Линейный выпрямитель. Если характеристика у -у(х) имеетйолее сложный вид, то вычисление моментов функции у уже нельзя свести к вычислению моментов функции х. Но тогда можно непосредственно вычислить

момент

y{t)y{t~z).