ТО за первое приближение следует принять то из чисел или by, для которого знак /(х) совпадает со знаком f {х), иначе говоря, нужно, чтобы в выбранной точке было / (х) / (х) > 0.

Замечание 1. Если f {x) меняет знак в промежутке (й, то может случиться, что вторые приближения окажутся хуже, чем первые (рис. 10.2). Поэтому полезно перед началом вычисления приближенно вычертить кривую у -fix). Однако иногда применяют метод Ньютона и тогда, когда / (х) меняет знак, или . даже вообще без всякого исследования. В таком случае получаемая последовательность приближений может сходиться

к корню или расходиться в зависимости от обстоятельств.

Замечание 2. Можно легко получить формулу (1), применив формулу Тейлора. Если Xq - точный корень, то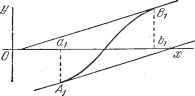

f{XQ) = f{by) + -{xQ-i

Рис. 10.2.

(Хо -ftl)2 +

Считая Xq - малой величиной и пренебрегая ее степенями выше первой, находим для Хр приближенную формулу. Это и есть формула Ньютона.

б) Способ пропорциональных частей. Удобно сочетать только что изложенный способ Ньютона со способом пропорциональных частей. Имея отрезок (йр by), в котором /(х) меняет знак, обозначим через а абсциссу точки пересечения прямой АуВу с осью х (рис. 10.1):

b,/{ay) - aj(b,)

а через 2 - абсциссу, полученную способом Ньютона. Найдя отрезок (а. Ь2). поступаем с ним так же, как с {ау, by), что дает нам а и /,3. Продолжая этот процесс, получаем две последовательности:

bj{ay) - aj{by) 2~ fiay)-f{by)

b2f (aj) - af {Ь)

/(й2)-/(*2)

b2 = by

h = b2

fib,)

f (b,y

fib,)

f (62)

которые все ближе и ближе охватывают с двух сторон искомый корень (если только fix) не меняет знака в промежутке {Uy, by)).

Замечание 1. Для того чтобы уже первые приближения по способу пропорциональных частей были достаточно близки к искомому корню, необходимо, чтобы f{x) не обращалась в интервале в нуль.

Замечание 2. Если иметь возможность все время точно вычислять fix), то приведенные выше способы позволяют находить сколь угодно далекие приближения и, следовательно, получать корень с любой точностью. Но если fix) находится из таблиц, которые неизбежно имеют лишь ограниченную точность, то и корень можно .получить также только с ограниченной точностью.

Пусть 8/(х) - совершенная при вычислении /(х) ошибка. Ова снижает точность вычисления х на такую величину ох, что

8/(х)-/(х)8х.

пример. Требуется решить уравнение хе-~2. Очень упрошенный чертеж показывает, что искомый корень заключен между О и 1 и вогнутость такова, что можно взять

аО. fti = l.

Имеем последовательности

а, = 0,

= 0,735, Сз = 0,8516. Й4 = 0,852625,

2 = 0,867, 3 = 0,8531, = 0,852627.

Если находить из пятизначных таблиц десятичных логарифмов с погрешностью, не превышающей 10 , то погрешность в определении / (х) будет того же порядка, атак как при л; = 0,85 ... /(х) == (1-4-х) е-* 3.3,

то Ьх=-- 10 = 3- 10 . Следовательно, нет смысла строить дальнейшие приближения.

10.1.3. Метод итерации. Напишем уравнение /(х) = 0 в виде

ф(Х)==ф(Х).

Грубое графическое изображение кривых

у = Ф(х), у = ф(х)

дает значение Xq абсциссы точки пересечения. Оно будет грубым приближением искомого значения корня. В действительности прямая х = Хц встретит рассматриваемые кривые в двух разных точках.

Возьмем ту из этих двух точек, для которой наклон касательной имеет меньшую по абсолютному значению величину. Положим, например, что

ф(Хо)< фио), (2)

и возьмем точку Хр, Уо = ф(Хо). Проведем из нее прямую, параллельную оси абсцисс, которая пересечет кривую у=:ф(х) в точке с координатами Xj, У(, = ш(х). Из точки Xj, Уо проведём параллель к оси ординат, которая встречается с кривой у -cp(x) в точке с координатами х, yj --.p(Xi). Оперируем с точкой Xj, У1 так же, как с точкой Xq, уд, и т. д.

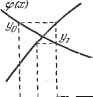Хд Х Xf

Рис. 10.4.

Если наклоны обеих кривых имеют вблизи точки пересечения одинаковый знак, то абсциссы Xj, Xg, ... стремятся к корню с одной стороны (рис. 10.3).

Если наклоны кривых имеют противоположные знаки, то абсциссы х х, ... принимают попеременно значения, то большие, то меньшие корня (рис. 10.4).

Поэтому искомый корень равен 3,00986 со всеми верными значащими цифрами.

Замечание. Остановимся, в частности, на применении метода итерации для решения алгебраических уравнений.

Пусть требуется вычислить корень полинома

близкий к Zq. Положим

XZ.- Zq.

Мы должны найти близкий к нулю корень полинома

f{x) = bQX +-b,X- ... +& jX + ft = 0.

Если коэффициент Ь у~ g{z не мал по сравнению с другими коэффициентами полинома /(х), можно принять

ф(х) = & 1Х, ф(х) = -Йо - ... - ft -2л: -

При этом

ф(0) = & !, ср(0) = 0

и эти величины сильно разнятся. Можно надеяться, что в точке пересечения кривых ср и ф, лежащей вблизи от точки х = О, наклоны кривых будут все еще сильно отличаться.

Пример. Вычислить близкий к 2 корень уравнения

3 -22 -5 = 0.

Положим

x = z - 4.

Получаем

/(х)=хЗ + 6х2+10х-1=0. Иначе говоря, требуется решить уравнение

cj (X) = I Ох = - хз - 6x2-f 1 = <f (х).

Легко заметить, что скорость сходимости тем больше, чем больше отли- . чаются наклоны кривых (риф.

Пример. Требуется вычислить вещественный корень уравнения

cos X = х - 4.

Построение кривых y = cosx, у = х - 4 показывает, что абсцисса точки встречи приближенно равна 3. Берем

9(x) = cosx, ф(х)=х - 4. Неравенство (2) соблюдено. Имеем последовательно