Последовательное дифференцирование дает

fU {X) = (X - а) (X) + pf- (X). / ij (а) = p/f(а) = I..... - k).

Следовательно,

r\a) = p/f- (a) = p(p~l)ff- (a)= ... =p!/,fa).

Bee свелось к нахождению величин /р(а) = -/ (а), которое выполняется по тому же образцу, что и нахождение /(а). Последовательно находятся величины

Co~bo = aQ, Ci = ft, + aC( C2 = ft2 + aCi...../i ( )= --ас 2.

hQ = go= =а. h,=gi+ahQ, h2 = gi+-ah,...../р(a) = g- p+a/z, p ,.

Вычисление производится механически, если расположить эти величины по приведенной здесь схеме Горнера:

где /j (х) - некоторый полином степени п - 1 (частное от деления / (х) на X-а):

/i(xJ = fto -4-ft,x -2 ... -l-ft i.

Отсюда

/ (X) = b,x + (ft, - afto) x -i + (ftg - afti) x -2 +...+(/( ) - aft ,). (9)

Отождествление (7) и (9) дает

Ьо=а, ft, = fl;i4-[xfto, ft2 = fl:2 + afti...../(a) = --aft ,.

Если нужно вычислить при х = а значения не только /, но и ее последовательных производных, построим по образцу ЛС- -) полиномы /2(х)...../ (-). определяемые тождествами

/,(х) = (х -а)/2(х)--/,(а). Д ,(х) = ,х-a)/(x)-h/ft i(a).

Пример. Дан многочлен /(х) = х5 +гОх - Юх + 2x2 - Зх - L&. Для а = - I схема осуществляется так:

10.2,3. Построение Лилла. Это построение осуществляет графически

операции, дающие коэффициенты Ь, by.....п = f {) из схемы Горнера.

Иначе говоря, оно графически дает результат подстановки числа а в полином

йо + й,х -1+ ... +fl ,xH-fl .

Дан квадрат MNPQ, стороны которого ориентированы в направлении, указанном стрелками (рис. 10.10). Выберем единицу длины и отложим от точки О

параллельно стороне MN отрезок длиной а. Если число положительно, то отрезок откладывается в направлении MN, если оно отрицательно, то в обратном направлении. Получаем точку Лр. От этой точки параллельно стороне NP откладываем отрезок длиной при той же договоренности о знаках. Получаем точку Ау. Продолжаем таким же образом построение, проводя параллели к последовательным сторонам квадрата. Получаем точки А, Лд, .. ., Л р Л . После этого из точки О проводим луч, образующий с лучом OAq такой угол 6, что tgO=a. Он будет, следовательно, справа от OAq при отрицательном а и слева - при положительном. Этот луч пересекает ААу в точке Bq. Восставим в Bq перпендикуляр к OBq, пересекающий Л,Л2 в точке By, и т. д.

восставленный что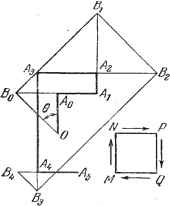

Рис. 10.10.

из точки В

Последний перпендикуляр пересекает прямую А уА в такой точке В

В -уА = f (а). Действительно, имеем

BQAQ=aQa, BQAy = aQa.-+-ay = by, BA-byo., ВуА2 = byo.-\-a2== b.

Получаем при этом алгебраическое уравнение /gfXg), один корень которого заключен между --1 и бесконечностью. Пусть 2 a+l-целых числа, между которыми лежит этот корень. Производим замену переменной

= а2~{- ~- и т. д. Искомый корень равен

X, = а,

, 1

cti-i---

Если он рационален, то эта непрерывная дробь конечна.

Пример. Требуется определить заключенный между -{-3 и --4 корень уравнения

/, (Xj)z=2x3 -3x2- I2xj - 1 =0. Положим Xj == 3 -(- -i-. Получаем уравнение

/2(х2)=10хЗ - 242 15x2 - 2 = 0,

корень которого, больший чем заключен меисду 2 и 3. На это указы-

вает то обстоятельство, что в ряду чисел /2(1). /2(2), ЛСЗ). ... впервые перемена знака наблюдается при переходе от /2(2) к /2(3). Положим

2--Т- -

Получаем уравнение

(Х3) = 48x3 9j2 2,вх -10 = 0. корень которого, больший чем --1, заключен между 1 и 2. Положим

Получаем уравнение

;Дх) = 7x1 - yOxj - Г65х - 48 = О,

Таким образом, операции первой строки схемы Горнера осуществлены графически. Если точка В , совпадает с Л , то a = tge таково, что /(а) = 0. Следовательно, а есть корень. Отсюда получаем способ нахождения на ощупь вещественных корней полинома.

Рис. 10.10 составлен для полинома

2x5-I-2х* - jc3 + 3jc2 - 5х Н-2;

тонкие линии показывают подстановку a=l=tg-. Находим ВА~3.

10.2.4. Способ Лагранжа. Пусть /](Xj) - алгебраическое уравнение, которое нужно решить. Предположим, что требуется найти корень а, заключенный между двумя последовательными целыми числами

1 и а,-+1.

Производим замену переменных

, 1

х, = а