Отсюда для первого интеграла при тФ п найдем

sin {п - т)х 6+2 1

и - т

sin {п-\- т) x п-\-т

При п = т имеем

е+2л

е+2л

У sin пх dx = 1 dx - Y У dx = t:. е G ё

Подобными же элементарными расчетами легко убедиться в справедливости соотношений (2) и (3).

Умножим обе части формулы для ряда Фурье на sin тх и проинтегрируем от 6 до 6 -j- 2к. Тогда *)

е+271 0 + 27Г , со оо ч

J f (х) sin mxdx = j sinmx + a sin rex + cos rex dx.

Согласно соотношениям (1), (2) и (3) все интегралы справа равны нулю, кроме

e+27t

J asinmxsinmxdx, e

который равен атг. Поэтому

е+2л

а = - 1 f (х)sinmx dx.

Аналогичный расчет дает

e+2,t

cos dx.

е+2л

bQ = -f f(x)dx.

2.!.2. Разложение в ряд по ортогональным функциям. Способ вычисления коэффициентов, описанный выше, может быть применен и в случае разложения в более общие ряды - в ряды по произвольной системе ортогональных функций.

Рассмотрим совокупность функций вещественной переменной

tti(x), uix), tt (x), ... Если эти функции таковы, что

/ т (Х) и (Х) ср (х) dx = о

при тФп, то принято говорить, что функции гг (х) образуют в проме-жзп-ке [а, Ъ\ ортогональную систему с весовой!) функцией ср(х).

*) Нетрудно показать, что при выполнении условий Дирихле ряд можно интегрировать почленно.

) Она называется также базовой функцией.

Пусть дана функция /(л:), удовлетворяющая условиям Дирихле. Она может быть представлена в виде бесконечной суммы ортогональных функций, т. е. ортогональным рядом вида

/(х) = С1Й1(х)+С2К2(х)+СзКз(х)Ч- ... + с к (лг) +

Чтобы вычислить коэффициент с, умножим обе части последнего равенства на и(х)ср(х) и проинтегрируем в промежутке [а, Ь\. Согласно формуле (7) все интегралы справа исчезают, кроме

откуда

f m ( ) f {- ) / М dx

J ul{x)ce(x)dx

Например, для полиномов Чебышева промежуток равен (-1, 4-1), а весовая

функция будет (1-х2) (см. п. 7.9.3). В некоторых случаях весовая функция равна единице, например для полиномов Лежандра (см. п. 7.6.9).

Если кроме равенства(7) функции м (х) удовлетворяют условию ft

f ul(x)f(x)dx = h (9)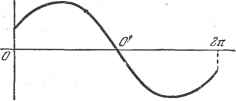

Рис. 2.1.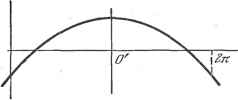

Рис. 2.2.

то система называется ортонорми-рованной. *

Основная тригонометрическая система функций

1, cos л:, sinx, cos2x, sin2x,

как следует из формул (1)--(3). ортогональна с весовой функцией, равной единице, но не ортонорми-рована.

2.1.3. Частные случаи. Если кривая, изображающая функцию,

имеет на оси Ох центр симметрии - точку О (рис. 2.1), то, приняв эту точку за начало координат, получим /(-х) - - /(х). Функция /(х) - нечетная, поэтому ее ряд Фурье должен содержать только синусы. Следовательно.

Если кривая, изображающая функцию /(х), имеет ось симметрии, то, приняв эту ось за ось ординат и выбрав начало координат в точке О, в которой ось симметрии пересекает ось Ох (рис. 2.2), получим /(х) = = /(-х). Функция /(х) - четная, поэтому ее ряд Фурье должен содержать только косинусы и постоянный член. Следовательно.

а ~а - ... = а ~ - = 0. .

2.1.4. Интегрирование и дифференцирование. Если функция удовлетворяет условиям, поставленным в начале главы, то ряд Фурье для интеграла от /(л:) получается почленным интегрированием ряда Фурье для функции /(л:). Ряд для производной /(л:) может быть получен из ряда для /(jc) почленным дифференцированием. Это верно, если только ряд для /(л:) является сходящимся, что бывает не всегда *).

Пример. Требуется разложить в ряд Фурье в промежзггке -к, -f- тг (6=- тг) функцию у=/ (л:), равную -1 при -< X < О и -- 1 при О < X < -- It. Из графика функции (рис. 2.3) видно, что точка О является центром симметрии. Следовательно,

Имеем

о 71

Рис. 2.3.

sin rex dx -

к

COS nx \ .

COS nx

- [1 -cos Ml = - [1

t. e.

2p + l- (2/Р+1)я

Отсюда получаем ряд

sinjc

sin 3jc

s\n(2p-\-l)x 2p+\

Производная заданной функции повсюду равна нулю, кроме твчки Х==0, где она обращается в бесконечность. Однако дифференцирование полученного ряда приводит к расходящемуся ряду.

Первообразная функция для функции у(х), Y = F {х), представляется сходящимся рядом

cos x

COS д>х

+...

cos(2jP+l)jt: (2p+\Y

- const.

График функции F(x) проходит (если константу справа счил-ать равнойнулю) через точку 0, -j. На рис. 2.3 он показан пунктиром.

Положим в предыдущем разложении х - 0. Получим формулу

- 1 Н~ Н~ 52 н~... ~\~

{2p+\f

Замечание 1. Если у = f (х)- непериодическая функция, то ряд Фурье совпадает с самой функцией только в промежутке от 6 до 6-)-21г. Если /(х)

*) Последнее замечание очень важно. При дифференцировании cos пх и sin nx члены ряда умножаются на п, что ухудшает сходимость. Подробнее см. [1], гл. 20, стр. 577-578.

**) В этом легко убедиться, если, в соответствии с рис. 2.3, проинтегрировать функцию у {х) от - до лг.