Если 2р=п, то система (41) допускает единственное решение. Все ошибки Sp {xD - У; равны нулю. Сумма квадратов ошибок, очевидно, также равна нулю.

Если 2/7 < , коэффициенты определяются условием сделать сумму квадратов ошибок наименьшей. При этом система (41) не удовлетворяется.,

Два последних случая можно рассматривать совместно. Вместо того чтобы решать систему (41), коэффициенты находят таким образом, чтобьг сделать сумму квадратов ошибок наименьшей. Если 2/? = ,этот минимуь4 равен нулю.

Сумма квадратов ошибок равна

г = 0

Р Р \12

У/ -(0+ 2 ftCos&x+ 2 asinkxi k=i ft=i

Коэффициент bf, определяется из уравнения У1 -

I дЕ \} ,

г = 0

0+ 2 й/С03&х.+ a.smkx

Если п-\-\ чисел делят интервал О, 2ii: на равные части, т. е. хо = 0, . .... х 1 = 2(и-1)-, х = 2тг.

(42)

0. (43)

и если к и -различные целые числа, заключенные между О и р то можно написать

2 sin/гх= 2 cos = О,

2 Sin kXi Sin kxi = 2 COS kx cos kxi = 2 cos kxi sin kx- =p,

in2i%X, = 2<0 = S - 2=°

t = 0

sin

j=0 i=0

Следовательно, формула (43) дает

t = 0 t = 0

1 = 0

Точно так же

1 = 0

Средняя величина квадрата ошибки равна

(44)

(45) (46)

1 = 0

11=1

Замечание 1. Мы предполагали до сих пор, что = у, иначе говоря, что функция у = / (х) не имеет точек разрыва первого рода в начале. Если Уо Уп чтобы уничтожить разрывность, достаточно из данной функции вычесть подобранную должным образом пилообразную функцию d (х) (рис. 10.11). Разложение этой последней функции в ряд равно

d{x) =

>о4-уя I уо -уд

sin X + Y sin 2х + ... + -i sin их + .

Замечание 2. Если бы мы захотели пользоваться способом, изложенным в предыдущем пункте, то, вычисляя методом трапеций интегралы, входящие в формулы (38), мы получили бы формулы (44) - (46).

10.3,13. Практические способы вычисления. Если таблица чисел, определяющих эмпирическую функцию, дана заранее, то дело сводится к вычислениям по формулам (44) - (46). Если же эмпирическая функция дана графически, то число и-f 1, которое служит для составления таблицы, находится в нашем распоряжении. При и =12 вычисления значительно упрощаются, так как фигурирующие в расчетах 24 значения синуса и косинуса с точностью до знака принимают лишь три значения, отличные от нуля:

Рис. 10.11.

0,5, 1 = 0,866,

Вычисление ведется при. этом следующим образом:

1. Записываем 12 значений функции:

/i /2 /3 /4 /5 /б /12 /и /ю /9 /в /7 Суммы . Sq Si S2 Sq

Разности ... dy d2 d;

2. Записываем суммы и разности:

4 5 6

0 1 2 3

Суммы ... 0 Разности ... §0 1 2 3. Составляем таблицы:

а) Вычисление коэффициентов при синусах

dy 2 3

6] 62 63 1 Ъ

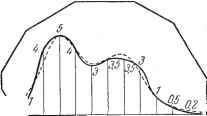в этих таблицах числа 0,500, 0,866, 1,000 умножаются на соответствующие (стоящие в той же строке) значения 6, т] или 8. Произведения в каждом столбце складываются. (Сложение и вычитание полученных сумм (I И и I-II) дает искомые коэффициенты и ft.

Графический метод. Можно пользоваться графическим методом для вы-

п+1 . /г4-1

числения величин -~- 6, --а,,

определенных формулами (44), (45).

Рассмотрим векторы с модулями yj, У2, ... и аргументами fexj, kx, ... О 1 г 3 5 6 7 в 9 W ]I1Z

Величины а, 6 будут соответственно проекциями на оси Оу и Ох геометрической суммы этих векторов.

Пример. Дана функция, изображенная на рис. 10.12, а. Вычисления коэффициентов и bj приведены на стр. 710.

Графический способ, применяемый на рис. 10.12, б, дает результаты, прекрасно согласующиеся с предыдущим вычислением. Чтобы не загромождать чертеж, ломаная линия, соответствующая определению % и Ь, не изображена.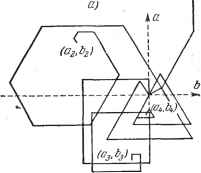

Рис. 10.12.

Если требуется найти более короткое тригонометрическое выражение S(x) - bQ+-bi cos л:-Ь 62 cos 2д: И-63 cos Зх-j-cj sin х + 2 sin 2д; + ag sin Зх, возможно лучще приближающееся к графически заданной функции, вычисление коэффициентов можно осуществить только сложением и вычитанием:

3 =(У4 - У2 + Ув - Уб + У12 - Ую)- 3 =-g-(У1 - Уз + У5 - У? + Уэ - Уп)

4Уо-Уб) -

2 = (Уо - Уз-f Уб - Уэ)-

б) Вычисление коэффициентов при косинусах