имеет период .tz, то ряд Фурье равен этой функции для всех значений х от - оо до -\- со.

В рассмотренном примере разложения для у и F представляют собой ступенчатую и пилообразную функции, графики которых указаны на рис. 2.4.

Рис. 2.4.

Замечание 2. В предыдущем примере функция f(x) разрывна - коэффициенты ее ряда Фурье имеют вид -. Функция F {х) непрерывна, но ее первая производная разрывна - коэффициенты ряда для F (х) имеют вид . Нетрудно обобщить это правило и показать, что если дана периодическая функция, непрерывная вместе с ее первыми р - 1 производными, и если ее р-я производная разрывна, то коэффициенты ее ряда Фурье будут порядка .

Пример. Разложим в ряд функции / {х) = cos ал: от - до тг (а - не целое число).

Функция f{x) - четная, поэтому все коэффициенты а равны нулю. Имеем

к

1 г , I ( sin (а + ) л , sin (а - и) я)

Ъ -- / cos ал: cos л: dx = - -7------\ =

2 . cos л 2 , 1 чи sin ая = -азшатг-5-(-1) ~-5-,.

откуда

cos ах =

2с1 sin ая г I

cos 2х

cos 2,х

а2 -Р

а2 -22

а2 -32

Приложение. Положим в предыдущей формуле х = тг и обозначим а через X. Разделив на simrx, получим

ctg ICX :

ctg тгх

2x2 2х

Х2-.12

12-Х2

Х2 -22 1

22-Х2

Х2 -32 1

Если X заключен в промежутке О < х <; а < 1, то общий член ряда внутри квадратных скобок меньше общего члена ряда

Следовательно, ряд внутри квадратных скобок сходится равномерно, и можно проинтегрировать обе части равенства от нуля до х. Освобождаясь от мйо-

жителя - и учитывая, что lim In = In д, имеем

sin itx

-НС--)

Символ JI означает бесконечное произведение. В данном случае это [зведение биномов вид Отсюда получаем формулу

произведение биномов вида 1 , п пробегает все целые значения

sin It л: = тех

2 \

(i-)... (10)

Если X придать значение у, получим формулу Валлиса:

л 2-2 4-4 2п-2п

2 -~ 1-3 3-5 (2и-l)-(2 -f 1)

\ 2.1.5. Случай, когда разложение в ряд Фурье ограничено первыми я членами. Дана функция f{x), определенная в интервале (6, В-2-к), и тригонометрический ряд, который оборван на первых п членах. Коэффициенты ряда произвольны. iVlbi можем спросить себя, какими должны быть эти коэффициенты, чтобы сумма первых п членов тригонометрического ряда лредставляла наилучшим образом функцию fix) в рассмотренном интервале. Пусть сумма первых п членов тригонометрического ряда равна

Snix)bQ-\- abSmkx-\- bfcoskx.

k=l k=l

Определим выражение для коэффициентов ряда а., Ьц так, чтобы величина Е=- У Ifix) - S ix)]dx - средняя квадратичная ошибка, которую мы

делаем, заменяя f(x) на 5 (х) в интервале от 6 до Ь~\-2я, - была минимальной. Для этого нужно коэффициенты и Ь выбрать так, чтобы

да, да2 ~ да ~ дЬо дЬ, . дЬ

) При помощи символа JJ бесконечное произведение

(l-b o)(l-f- ,)(l-f- 2) ...(1-h )..-

люжет быть кратко записано в виде

-Й + -

Логарифм бесконечного произведения равен сумме ряда, о.щий член которого -!n(l-f-k ). Так как ряды !n(l-f-k ) и и одновременно сходятся или расходятся, то можно сформулировать следующее положение.

Произведение JJ (1 -f- w ) имеет при бесконечно возрастающем п предел, не

равный нулю и не зависящий от порядка сомножителей, если ряд, общий член которого равен и , абсолютно сходящийся. Такое лроизведение называется абсолютно сходящимся.

sin их

Обратимся к коэффициенту а. Он определяется из уравнения - = 0:

и+2к

дЕ дЕ

дйгг,

= -/(X) -asinftx -2]&;cosAx

sinmx dx= 0.

Это дает нам

откуда получаем

Z [/W - asinmx]sinmxdx = 0.

е+2,и

т = \ f fix) Sin mxdx.

Следовательно, разложение в ряд Фурье не только точно представляет функцию fix) при неограниченном числе членов*), но и обеспечивает наименьшую среднюю квадратичную ошибку по сравнению с любым тригонометрическим рядом по sinftx и cosftx, если эти ряды обрывать на произвольном конечном числе слагаемых. Замечательно, что при увеличении числа членов в конечной тригонометрической сумме S (x) все прежние коэффициенты сохраняют свой вид.

Замечание. Рассуждения остаются точно такими же, если речь идет о разложении в ряд по произвольной системе ортогональных функций uiz). Это означает, что мы получим наилучшее представление функции /(х) в виде ограниченного ряда по ортогональным функциям, если коэффициенты разложения определим по формуле (8). И здесь при увеличении числа членов в конечной сумме прежние коэф-

фициенты сохраняют свой вид.

2.1.6. Изучение разложения в ряд Фурье вблизи точки разрыва. Явление Гиббса. Пусть у = fix) - функция, имеющая разрыв в точке х = а (см. рис. 2.5):

lim / (а - е) = А, Пт/(а + е) = Б.

e-s.0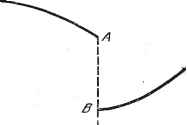

Рис. 2.5.

Введем в рассмотрение О (х) - функцию, имеющую значение - 1 при -7с<х<0и +1 при О < X < тс. Ряд Фурье для 0(х) будет

sin Зх ,

0(х) = 1Р

. sin(2n-1)х f 2/г-1

Функция fix) может быть записана в виде

/ ix-) = О (X - а) + /i (X).

*) В том смысле, что при п->схэ lim£ = 0.