Применяем измененный способ Пикара. Имеем <р(х) = 3, ф(х) = -2,

-откуда первое приближение получается из уравнения

:3у -2.

иначе говоря. Второе приближение будет

- 2,1,

+ 8х + 4еЗ + + 4

Сравниваем четвертое приближение Уд, второе приближение yj и точное решение у для х = 0,2.. Имеем

у (0,2) = 1,29099, yj (0,2) = 1,28776, Уз (0,2) = 1,28676.

Из этого примера видно, что при использовании способа Пикара хорошее начальное приближение приносит значительную выгоду.

10.7. ГРАФИЧЕСКОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

10.7.1. Дифференциальные уравнения первого порядка. Способ изоклин. Дано дифференциальное уравнение <р(х, у, у) = 0. Решив его относительно у, получаем у = /(х, у).

Будем, предполагать, что /(х, у) - однозначная функция х и у, имеющая конечные первые производные по х и у. Геометрическое место точек плоскости, в которых интегральные кривые имеют крутизну (т. е. тангенс угла наклона касательной), равную р, - это, очевидно, кривая

р = /(х, у).

Ее называют изоклиной. Если построить изоклины легко (в противном случае способ не представляет интереса), можно начертить на плоскости несколько изоклин /р 1р, ..., соответствующих крутизнам Ру, Р2, ...

Пусть Мд - точка с координатами Xq, (начальные условия) и пусть

Р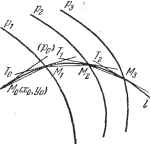

Рис. 10.13.

Ро = /(Хо. Уо)

--крутизна интегральной кривой, проходящей через эту точку; -ближайшая изоклина (рис. 10.13). Требуется найти точку My пересечения интегральной кривой с изоклиной /р,. Известно, что крутизна интегральной кривой в точке My есть ру. Поэтому мы заменим участок ММу интегральной кривой

на прямолинейный отрезок с крутизной, имеющей среднее значение ° .

Проведя через Mq прямую с такой крутизной, найдем точку My как пересечение этой прямой с изоклиной /р,- Потом проведем через My прямую

с крутизной P~Pi и в пересечении ее с изоклиной /р найдем точку Tkfg и т. д.

Гладкая кривая I, проведенная через точки М, М . .., будет приближать искомую интегральную кривую. При этом ломаная TkfoTHjTUg - - - вписана в 1. Описанную ломаную MqTqTiT2 . .. получим, проведя через точки Mq, My М2, .. прямые с крутизнами р, р Р2, . -., касательные к 1.

Полезно получить некоторые сведения о форме пучка интегральных кривых, облегчающие его построение.

Место точек перегиба. На каждой изоклине может находиться точка,

в которой интегральная кривая касательна к ней. В такой точке крутизна

интегральной кривой, равная /(х, у), удовлетворяет уравнению-4- =0, справедливому для крутизны изоклины. Поэтому в такой точке

dy df dy df Так как на интегральной кривой =

dx ду рассматриваемой точке т- е. интегральная кривая имеет перегиб при условии, что

отлично от нуля, чтобы имела место перемена знака кривизны .

Таким образом, /. --=0 есть уравнение места точек перегиба

интегральных кривых.

В случае, если дифференциальное уравнение не разрешено относительно производной <р(х, у, у) = 0, место точек перегиба получается исключением р

из уравнений <р(х, у, р)~0 и -ч-Р == 0.

Место точек возврата. Положим, что пучок изоклин имеет огибающую. Тогда }фавнение этой огибающейможно получить, исключив р из уравнения изоклин <р (х, у, р) = 0 и = 0. Изоклины, касательные к огибающей, находятся вблизи нее с одной ее стороны. Интегральные кривые, проходящие вблизи огибающей, не могут ее пересечь, и в большинстве случаев точка, общая с огибающей, является для них точкой возврата.

Если изоклины имеют двойную точку, то в этой точке интегральная кривая возвращается с той же крутизной. Следовательно, это точки, где интегральные кривые касательны сами к себе. Если это имеет место, то уравнения

. -Й=0, = 0, ,(х,у.р) = 0 .

совместимы, и исключение р дает искомое место.

Асимптоты. Если пучок интегральных кривых имеет общую асимптоту,

то при бесконечном возрастании х предел и будет один и тот же.

Заменим в дифференциальном уравнении у на р и у на рх. Тогда

<р(х, рх, р) = 0.

Если при бесконечно возрастающем х величина р, полученная из этого уравнения, имеет пределом Ру то прямая y = /7jX-}-j - асимптота, если значение q, полученное из

fix. PiX-+q. Pi) = 0

при бесконечно возрастающем х имеет конечный предел j. Если же предыдущее уравнение не зависит от х, те прямая у = pyX-\-qi входит в пучок интегральных кривых. Это особое рещение, которое обычно входит в огибающую пучка.

Пример. Дано у=х2 - у.

В той части плоскости, где х - у <. О, интегральных кривых нет. Через точку, где х2 - у2 ~> о. проходят две интегральные кривые, крутизны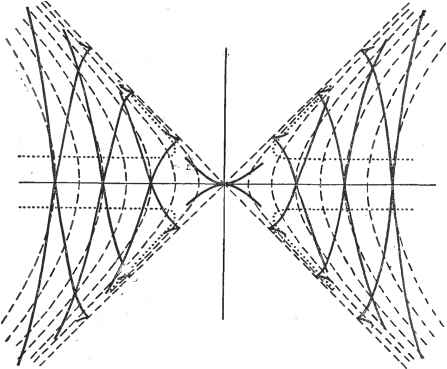

Рис. 10.14.

которых противоположны. Пучок интегральных кривых симметричен по отношению к осям Ох и Оу.

1. Изоклины. Это гиперболы х - у2 = р2.

2. Место точек перегиба. Из х - у-р и 2х - 2ру = 0 исключают р. Тогда х2=у2(х2 - у2).

Дважды продифференцировав дифференциальное уравнение, получаем

2уу + 2у = 2 - 2у - 2уу .

Условие у = 0 не влечет за собой у =гО. Следовательно, кривая х2= = у2(х2 - у2) и есть место точек перегиба.

3. Для изоклин нет огибающих.

4. Место точек возврата. Исключим р из рх - у и 2/7 = 0. Тогда получим х -у2 = 0, иначе говоря, биссектрисы осей координат. Здесь изоклины не имеют двойных точек. Значит кривая х - у2 = 0 есть место точек возврата.

5. Уравнение горизонтальной касательной к интегральной кривой - это - у2 = 0. Следовательно, в точках возврата касательная горизонтальна.