примененное к точкам а, Ь, с, d, дает

(108)

После того как обе эти задачи решены, можно взяться за основную задачу. Разложим область внутри заданного контура на некоторое число прямоугольников. В уравнении (105) следует заменить частные производные приближенными формулами (108) или (107). Мы получим таким образом уравнения, которые дают возможность вычислить значения U в точках внутри контура как функцию значений U на контуре, данных из условий задачи.

Формула (107) применяется главным образом в центральной части зоны, ограниченной контуром, там, где узлы прямоугольной сетки являются равноотстоящими. Формула (108) применяется в основном в периферической части этой зоны, если близость границы вносит неправильность в положение узловых точек прямоугольной сетки (рис. 10.19).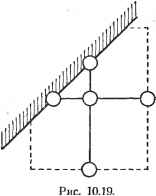

13 /-1 16

-1-i i

-л- i i

26 2/,

28 2ff 30

Рис. 10.20.

Пример.. Рассмотрим очень простой пример. Требуется найти функцию и, принимающую соответственно значения +1 и -1 на двух прямых углах, определяемых точками 19, 13, 7, 1, 2, 3, 4, 5 и 12, 18, 24, 30. 29, 28, 27, 26, и удовлетворяющую уравнению Лапласа внутри прямоугольника (рис. 10.20). Сетка образована квадратами {k=:l). Если перенести в урав-

и у j из формулы (107), то получим 4Ui = U, + U,~\-U-hU,. Применим это выражение к 12 точкам внутри прямоугольника. Тогда

*) Если учесть симметрию задачи, число уравнений и неизвестных можно уменьшить вдвое.

) То, что в английских и американских работах называется методом релаксации . - , , . .

U, = U, = U, = U, = U\ = [Ji, = U\,\.

tl2 = tlS = 24 = 29 = f28 = 27 = U2e-l.

Предыдущая система принимает вид

4t/ = t/io+i7i,. 4t/,4=t/i5 4-t/8+t/.2o-f 1.

4t/,5=:t/,4+f/i6+t/9+t/2

4t/i, = t/-,e+t/ii+t/23-l.

4t/-. = t/2, + t/i4,

4t/2, = t/2o+t/22+t/i5-l,

4t/-22=t/2i+t;-23+t/i6-l.

4t;-23=t/22+t/ -2*).

Можно попытаться прямо решить эту систему из 12 уравнений с 12 неизвестными. Однако для более сложных систем, где внутренние точки насчитываются сотнями, надо решительно отказаться от этого способа и применять следующий способ последовательных приближений

Мы будем обозначать первое, второе, ... приближение U в точке а через Ua, Ua, . Значения, взятые в качестве начальных для внутренних точек, могут быть любыми, но удобнее выбирать значения, не слишком отличающиеся отрезультатов вычислений. Простое рассмотрение рисунка подсказывает нам выбор в качестве начальных значений:

t/l4 = t/8 = t/9 = t/jo=+0,5, 21=t/22=t/23=i7i,= -0,5.

Перенеся эти значения в предыдущие уравнения, получим первые приближения:

4Us=:Ug +t/i4 + 2 =0,5 +0,5 4-2=3 , t/8 = 0,75,

4t/9=t;8 -Ht/,o-bt/i5-bl =0,75 +0,5 + 1 =2,25. t; = 0,562,

4t/;o = t/9 +t/n + t/i6+l =0,562+ 1 =1,562, t/io= 0,390,

4t/n = t/w + t/i7 =0,390 - 0,5 =-0,110, t/n = -0,027,

4t;;4 = t/i6+f/8 +t/2o+ 1 =0,75 + 1 = 1,75, t/m= 0,437,

4t/ls = t/i4+ t/i6+t/9+t2i=0,437 + 0,562 -0,5 = 0,499, t/i5 = 0.125.

4Ui6 = Ui5 + Un + Ulo + U22 = од 25 - 0.5 + 0.390 0.5 = - 0.485.

4Un = Uie-\-Uii-\-U23-l = - 0,121 -0.027 -0.5-1 =-1.648.

un = ~0Al2,

4Uw = U2i~\-Uu =-0.5 + 0,437 = -0,063. t/= -0,016.

iU2i = Uw + U22-\U[b- 1 = - 0.016 -0.5 + 0.125-1 =- 1,391,

t/2i= -0,348,

4t/22 = t/2i + Lf23 4-t/i6-1 = - 0,348 - 0,5 - 0,121 - 1 = 1,969,

U22 = - 0.492.

4t/23 = t/22 + tn - 2 = - 0.492 - 0.412 - 2 = - 2.904.

t;- = -0.726.

Затем получаем вторые приближения:

4t/8 =fy9 + /724 + 2 =0,562 + 0,437 + 2 = 2,999, ul=Q.7bQ,

4Us = t/8 + t/io+t/i5+ I =0,750 + 0,390 + 0,125+ 1 =2,265,

Us = 0,566.

4Uio = Uq + t/n + t/i6 + 1 = 0,566 - 0,027 - 0,121 + 1 = 1,418,

t/10 = 0,354.

и т. д. Продолжив вычисления до пятого приближения, получим таблицу:

Точки

8 9 10 11

14 15 16 17 20 21 22 23

Приближения и

исходное

первое

второе

0,5 0,5 0,5 0,0 0,5 0,0 0,0 -0,5 0,0 -0,5 -0,5 -0,5

0,750 0,562 0,390 -0,027 0,437 0,125 -0,121 -0,412 -0,016 -0,348 -0,492 -а,726

0,750 0,566 0,354 -0,014 0,465 0,140 -0.102 -0,460 0,029 -0,331 -0,540 -0,750

третье

четвертое

пятое

0,758 0,563 0,362 -0,024 0,482 0,153 -0,121 -0,474 0,038 -0,337 -0,552 -0,754

0,761 0,569 0,356 -0,029 0,488 0,150 -0,130 -0,478 0,038 -0,341 - ,555 -0,758

0,764 0,567 0,352 -0,031 0,488 0,146 -0,134 -0,481 0,037 -0,343 -0,559 -0,760

10.8.2. Задачи вращения. В предыдущем пункте речь шла об отыскании и как функции декартовых координат х, у. Здесь стоит та же задача для цилиндрических координат гиг. Однако имеются некоторые отличия, которые будут изложены ниже.

Рассмотрим разложение в ряд (106). ограниченное членами второго порядка, и заменим х на г:, а у на г. Мы получим следующие группы формул, тождественные до виду с уравнениями (107) и (.108).