А + В

где - функция, уже не имеющая разрыва при х = а /j(a) =

Поэтому для изучения особенности разложения /(х) вблизи х = а достаточно рассмотреть поведение 0{х) вблизи нуля.

При X = О О (х) имеет своим значением ±1 в зависимости от того, как X стремится к нулю: принимая положительные или отрицательные значения. Сумма же ряда Фурье для О (х) при х О стремится к единственному значению - нулю. В этом нет ничего удивительного, так как ряд справа-непрерывная функция х и не может иметь двух разных значений при значении переменной х = 0.

Рассмотрим первые п членов разложения Q\x):

с f \ 4 rsinx I sinSx sin (2n-l)x

Начертим кривую, представленную этим рядом. Для этого изучим производную 5(х):

(х) = [cos X 4-cos Зх 4- ... -f-cos(2re-1)х]. Если, в формуле (1) п. 1.1.13 положим 8 = 2х, а cos х--cos 3x4- - + cos(2re- 1)х = Следовательно,

X, то

cos пх sin пх 1 sin 2пх

sinx

2 sinx

sin 2nt sint

Максимумы и минимумы S (x) при изменении х от О до определяются

равенством sin 2пх = 0> откуда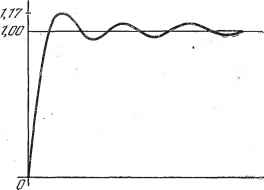

X =

(/г= 1, 2..... ).

Кривая S (x) совершает ряд колебаний вокруг ординаты у = (рис. 2.6). Нетрудно заметить, что первый максимум (при k=\) наибольший. Его ордината равна

sin 2nt sin

sin у dy

2n sin 2n

где мы обозначили у = Int. Рис. 2.6. При больших значениях п

(соответственно малых х) можно

заменить sin на Предел ординаты первого максимума при ге->оо

(х->0) будет, следовательно,

ГС

2 Г sin у , 2 .

- / -dy = -811;;=: 1,179...

вместо того, чтобы быть равным единице (символ Si обозначает интегральный синус - см. п. 7.2.1).

Таким образом, функция, представленная тригонометрическим рядом, переходя через разрыв, делает скачок, примерно на 18% больший, чем исходная функция. Это явление было обнаружено в 1899 г. американским физиком Гиббсом. Оно иллюстрируется рис. 2.7, где приведены графики функций S (х) - сумм п первых членов разложения в ряд Фурье функции 0(х) -для п=1, 3. 7, 15, оо в промежутке [О, тс]. Из-за явления

/7=Щ 75,7,3,7 7,77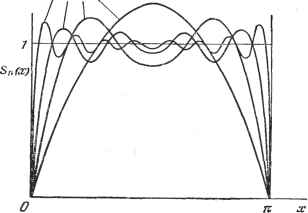

Рис. 2.7.

Гиббса представление разрывных функций рядом Фурье в окрестности точек разрыва не вполне удовлетворительно *).

2.1.7. Случай произвольного промежутка. В случае, если период функции f (t) равен не 2ir, а Т, то ее следует рассматривать в промежутке не от 6 до 6 4-2, а от 6 до 6+Г. Тогда

/ (f) = *0 + 2 cos я ш/ 4- 2 г ~

Коэффициенты равны

b =-jT f {t) cos пЫ dt,

a =Y f f(.t)sinnwtdt, ё

(11)

(12) (13) (14)

2Td **)

Эти формулы совпадают с (4) - (6), если заменить там х на-

*) Подробное изложение явления Гиббса дано в [1], стр. 490-495. **) При вычислении интегралов от периодической функции / (t) можно считать е=;0.

Ьп Jan у /(0(со5пш-ysinreiuOdf / f (t)eidt,

Здесь отметим два обстоятельства:

. - ia b -\- ia

1. Из формулы для 2 можно получить выражение для .

изменив к на - п. Если первый коэффициент обозначить через с , то второй должен быть обозначен как с .

2. Постоянный член можно написать в таком виде: Ь = j f{t)e°dt.

Он получится из общей формулы, дающей с± , если положить в ней п-0. Следовательно,

f(t)= 2 ceJ-t (15)

/г= -со

п = т f fit)e-J--idt. (16)

Выражение (15) представляет собой разложение в ряд Фурье с комплексными членами, а (16) - формулу для коэффициентов, которые участвуют в этом разложении. Мы получаем, таким образом, внешне более простой ряд, чем разложение с вещественными членами. Он имеет то преимущество, что коэффициенты разложения определяются одной общей формулой. Б разложении с вещественными членами это не имеет места.

2.1.9. Графическое представление. Спектр. Если положить a = s sirif и & = s cos9 , то ряд (11) функции f[f) получает вид

/ (О = + 2 s COS {пЫ - 9 ).

Функция f(f) разложена в сумму гармонических компонент; s и 9 представляют собой соответственно амплитуду и фазу отдельных гармоник.

Эти гармоники можно представить в векторной форме. Если расположить разные векторы, соответствующие каждой круговой частоте, вдоль

2.1.8. Ряды с комплексными членами. Пусть

со со

f (t) == a sintnot-\- Ь COStiiot + bQ.

n=1 . я=1

Имеем

со со

П=1 я=1

где на основанш? формул (12) - (14)

0+7- е+г