некоторой оси, то мы получим трехмерное представление гармоник разложения в ряд Фурье. На рис. 2.8 оно дано для момента =0. Такое представление, однако, не очень удобно. Поэтому его обычно заменяют двум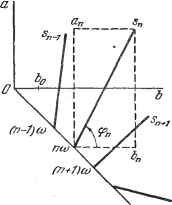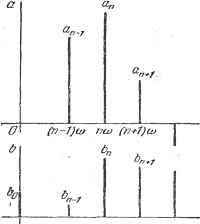

Рис. 2.8.

fn-7)tO ПО) fn-1JaJ Рис. 2.9.

(рис. 2.9), которые являются проекциями совокупности предыдущих векторов соответственно на плоскости фаз у и нуля, иначе говоря, представлением величин а и вдоль оси круговой частоты. Можно даже ограничиться представлением одних только длин s или их квадратов, опуская фазовые соотношения отдельных компонент. Такое представление называют спектром функции f {t) или, чаще, линейным спектром функции.

Что касается трехмерного представления на рис. 2.8, то здесь уместно сделать следующее замечание: если принять за новое начало отсчета времени момент то картина, изображенная на рис. 2.9, изменится, но длина векторов на рис. 2.8 останется неизменной. Каждый вектор повернется только на угол гешо, а вся совокупность векторов претерпит нечто вроде винтообразного скручивания. Поэтому представление, состоящее в том, чтобы изображать только модули s или их квадраты s, удобнее, так как оно инвариантно по отношению к изменению начала отсчета времени.

Возьмем ряд функции f (f) с комплексными членами (15). Совокупность комплексных величин с может быть точно так же изображена в трехмерной векторной форме. Вещественная и мнимая части векторов с играют ту же роль, что и коэффициенты а и Ъ, со следующим различием. Рис. 2.8 должен быть продолжен в сторону отрицательных круговых частот. Формулы

дают

R(c ) = Y . R(c ) = -2- . I(c )=-2-а , I(c ) = fl .

приводит к очевидной симметрии картины. Аналогично представлениям-рис. 2.9 проекции на плоскости фаз и нуля образуют удобные для-

работы представления (рис. 2.10). Приведенные выше замечания относительно влияния смещения начала отсчета времени действительны и в случае разложения с комплексными членами.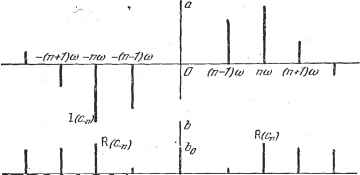

Рис. 2.10.

2.1.10. Среднее значение произведения двух функций одного периода, разложимых в ряд Фурье. Даны

со +CO

т~\ m=-co

со Ч-со

tn=\ т~ -со

Исходя из формул (1) - (3). отнесенных к периоду Г = -, нетрудно заметить, что

со Ч-со

Отсюда получаем

j {f{t)tdt = bl+\Yial+bl)= 2 (18)

о т=\ т= ~оо

Так, например, если cf>(t) - периодическая электродвижущая сила, приложенная к цепи, а f(t) - текущий по этой цепи ток, то среднее значение произведения - это средняя мощность, расходуемая в цепи. Она выражена в формуле (17) с помощью коэффициентов обоих разложений в ряд Фурье. Выражение (18), умноженное на R, дает среднюю мощность Р. расходуемую на сопротивлении R циркуляцией переменного тока f(t). Эффективная сила тока гэф в этом случае определяется из формулы

Заметим, что Ь-это интенсивность постоянной составляющей тока, а у -g-( а,п + raj = гш - интенсивность гармоники тока т-го порядка. Формула (18) при этом дает

iэф=Vbl-i-hq+ ... ....

а-Ит- I (p(x)sinmcoxdx,

6 = lim / 9 (x) cos mcox dx.

Таким образом, коэффициенты разложения в ряд Фурье функции 9(х) можно вычислить и не зная периода этой функции. Это наводит на мысль, что коэффициенты рд, р, получаются из соотношений

%==Пт f fix)dx.

S->oo

Pmlim-o- / /(Х)С05Ш ,Х6Х.

2 г

a =lim- / / (x) sin шх dx.

) P. Levy, Cours dAnaiyse, t. 1, p. 183. 1930.

2.1.11. Распространение ряда Фурье на почти периодические функции Рассмотрим функцию f (х), представляющую собой сумму периодических функций ./2W. ftiM периодами z, xg, т3, , т

соответственно. Если периоды соизмеримы между собой или, иначе говоря, они являются целыми кратными некоторого числа Т, то это Т и будет периодом функции /(х). В противном случае функция /(х) не периодична.

Однако если разложить функции /i(x), /2(л:), / (х) в ряды Фурье и просуммировать эти ряды, то мы получим разложение вида

/ (л) = -t- S Фт COS ш х -1- sin ш х).

Оно внешне походит на разложение в ряд Фурье, но это не ряд Фурье, потому что множители ш, - коэффициенты при х - не целые кратные одного числа.

Попробуем вычислить коэффициенты Ро> Рт- °m Рассмотрим ряд Фурье некоторой периодической функции ср(х):

cf>{x)== 2 cos шхН-а sin шх).

Согласно формуле (14) коэффициент равен среднему значению функции ср(х) по периоду, но он равен также среднему значению функции <{х) по бесконечному интервалу:

lim - / 9(x)dx.

S->co 5

Мы можем, следовательно, вычислить Ь, не зная периода функции <р(х). Точно так же, заметив, что соотношения (12) и (13) являются не чем иным, как средними значениями по периоду функций 9(x)sinm(ox и (f(x)cosmwx, мы получим коэффициенты а и из соотношений