2.Й ИНТЕГРАЛ ФУРЬЕ 101

f(t)= 0(т)е Am, 0{m)=J f (х)е-dx.

Оба эти выражения справедливы при--2 2

Пусть Т бесконечно возрастает. Тогда в пределе

f{t)= f О (со) е- du>, (20)

- СО

(21)

Если подставить выражение (21) для 0(ш) в формулу для f(t), то

-Ьсо -J-CO

f(i) = i f dm f fe -dx.

Последнее выражение представляет собой комплексную форму интеграла Фурье.

Отделим вещественную часть от мнимой:

+ 00 +СО +00 +00

J dw f /(T)cos(o(f-T)dT + y J du> J fix)sm(i>(t-x)dx

Функция sin(o(# - x) - нечетная функция от со. Отсюда вытекает, что мнимая часть полученной формулы равна нулю. Это, впрочем, очевидно, так как f(t)-вещественная функция и мнимая часть справа должна отсутствовать. Точно так же, поскольку cosco(? - г) - четная функция от со, мы можем, введя коэффициент 2, свести область интегрирования по ш к интервалу [О, оо). Следовательно, в конечном счете

со +СО

f(t)=f dco f f(x)cosm(t - x)dx.

о -co

Это в точности формула (19), найденная нами ранее.

Было бы интересно получить выражение интеграла Фурье в комплексной форме, используя амплитудную функцию Л(ш) и фазовую Ф(ш), определенные в п. 2.2.1.

Очевидно, что

G(< )=JL(o))e--* >.

откуда

+ СО

= i / . (22)

102 РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ [ГЛ. II

Замечание. Множитель можно поместить в любую из формул (20)

или (21): в выражение для 0(ш), как в данном пункте, либо в выражение для f (t), как будет сделано в п. 2.2.8, в соответствии с принятым стандартом для формул преобразования Фурье. Некоторые авторы из соображений

симметрии вводят множитель в обе формулы. Все это вопрос опреде-

ления 0(0)), иначе говоря, зависит от смысла вводимых в теорию обозначений. Здесь следует быть весьма внимательным, в частности, при пользовании таблицами преобразований Фурье.

2.2.3. Применение к электрическим цепям. Положим, что функция f (f) представляет собой электродвижущую силу, приложенную к контуру или электрической цепи. Согласно формуле (20) можно рассматривать электродвижущую силу f(f) как сумму бесконечного числа синусоидальных составляющих, амплитуды которых даны выражением 0(ш)(, а частоты проходят весь спектр от -со до -1-оо. Следует считать, что эти элементарные синусоидальные электродвижущие силы приложены бесконечно давно. Поэтому единственным электрическим током, который существует в цепи, будет ток с постоянным синусоидальным режимом. Действительно, переходной ток, вызванный внезапным приложением элементарной электродвижущей силы, экспоненциально затухает и в стационарном режиме равняется нулю. Конечно, для этого нужно, чтобы сопротивления цепи были положительны, иными словами, чтобы это была рассеивающая цепь. Итак, нас будут интересовать только синусоидальные токи.

Известно-, что если представить через Z(y(o) полное сопротивление контура или эквивалентное полное сопротивление цепи, а через £ов-°* -синусоидальную электродвижущую силу, то стационарный синусоидальный ток будет равен

Z(

Применим эту формулу к сумме синусоидальных электродвижущих сил, представленных формулой (20). Электродвижущая сила, соответствующая частотам, заключенным между со и ш--й(о, будет

G(o))e- do).

Результирующий стационарный синусоидальный ток, вызванный такой электродвижущей силой, равен

dm.

Сумма этих токов даст реакцию контура или цепи на электродвижущую силу /(О- Суммарный ток выражается равенством

+ 00

Если полное сопротивление контура или эквивалентное полное сопротивление цепи выразить через модуль и фазовый угол

Z(yo)) = fi(o))e< >,

то формула (22) дает

(>- 2я J iB(o>)

[<0<-Ф(т)-Р(ш)1

(23)

Пример. Электродвижущая сила f(t), разложение которой в интеграл Фурье дано формулой (22), приложена к зажимам усилителя. Коэффициент его комплексного усиления дается выражением

Б(<.)е Р .

Пусть функции, характеризующие изменение амплитуды S((u) и фазы Р(ш), представляют собой соответственно четную и нечетную функции от величины ш (рис. 2.12). Величина С на рисунке имеет размерность времени,

у можно трактовать как полуширину

полосы пропускания.

Форма выходного сигнала усилителя может быть представлена формулой (24), аналогичной (23):

е(0 =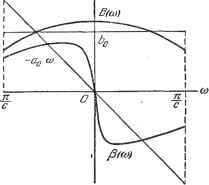

(24)

Если бы это был идеальный усилитель, то четная функция В(и>) свелась бы к постоянной (усиление, не зависи- Рис. 2.12.

мое от частоты), а нечетная функция

Р (ш) к линейной функции - аш (фазовый сдвиг пропорционален частоте). Разложим в ряд Фурье разности между идеальными и реальными функциями. Имеем

(ш) = И- 2 *й COS КСШ. п = 1

Р (ш)г= - йцШ + 2 т=1

Тогда формула (24) принимает вид

у° - со -

e(i) = J Л(ш) Ь,+ {е +е- П X

Е ja sin теш

Но известно (см. п. 7.5.11). что