Если подставить это разложение в предыдущую формулу, то мы в соответствии с (22) представим выходной сигнал e{t) с помощью членов вида .

f{t - ao~\r kmc) Vfe (aJ. f (t -- a, - kmc) (-1)* Vfe (aJ,

- f{t - ao±nc)J(aJ. fit-a,±nc-\- kmc) (aJ. f(t-a,±nc- kmc). i-\fJ (cj.

Таким образом, основной сигнал оказывается окруженным на расстояниях, кратных с, рядом паразитных сигналов.

т, п. ft= 1, 2, 3, ...

Рис. 2.13.

Картина будет более наглядной, если мы ограничимся в каждом из рядов (для Б(ш) и Р(со)) только первыми членами. Тогда остается только

Vo( i)/( - о)

(т. е. входной сигнал, запаздывающий на и умноженный на постоянный коэффициент) и еще сигналы вида

А Уо(а,) + Vi ( i)] f(t - a+ с).

А Уо ( 1) - Vi ( i)J fit - %- с).

изображенные на схеме рис. 2.13.

2.2.4. Случай незатухающей цепи. Во всех предыдущих рассуждениях предполагалось, что речь идет о рассеивающих электрических цепях, т. е. что все корни характеристического дифференциального уравнения, определяющего систему, имеют отрицательные вещественные части. Если.же корни чисто мнимые, то интеграл

не будет сходиться, так как Z{Jis>) становится равным нулю при вещественных значениях ш, следовательно, внутри интервала интегрирования. Чтобы найти, однако, решение в этом важном случае, обычно достаточно ввести

малый коэффициент затухания, вычислить ответ, а затем устремить коэффициент затухания к нулю:

3-*0

2.2.5. Спектр частот. Имея функцию О (со), мы можем определить-спектр частот функции f (t), аналогичный спектру ряда Фурье в комплексном виде, с той разницей, что здесь речь идет о непрерывном спектре. При частном значении со функция О (со) может быть представлена вектором, компоненты которого будут действительной и мнимой частью О (со). Если расположить начало этих векторов, соответствующее всем значениям со от - оо до +СЮ, на оси Осо, перпендикулярной плоскости хОу, образованной действительной и мнимой осями, то конец вектора 0(ш) опишет кривую-(в большинстве случаев пространственную), которая и будет графически

представлять непрерывный спектр частот функции f(t) (рис. 2.14).

Это трехмерное довольно неудобное изображение заменяют проекциями кривой О (со) на плоскости хОи>, уОю, т. е. кривыми.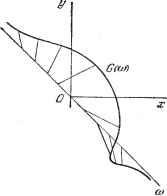

Рис. 2.14.

Рис. 2.15.

представляющими отдельно вещественную R(co) и мнимую 1(ш) части комплексной функции 0(ш) (рис. 2.15):

ч-со +00

R (со) =г У / {%) COS (ОТ d-z, !( >)- - У / (

Эти две кривые полностью осведомляют нас об амплитуде и фазе каждой составляющей. I (ш) - нечетная функция, иначе говоря, начало координат будет центром симметрии кривой 1(со). R((o) - четная функция, иначе говоря, ось ординат Оу будет осью симметрии кривой R((o). Отсюда вытекает, что если /(О- четная функция, то спектр сводится только к действительной

части R((o), совпадающей с модулем функции 0(ш), или с амплитудой

Точно так же, если /(О - нечетная функция, то спектр сводится к мнимохг

части 1((о), которая совпадает в этом случае с G((o) = .

Л10ЖН0 пользоваться также и другим представлением, которое состоит в том, что по оси ординат откладывают либо амплитуду

= 1G (co)l = IR2 (со) + Р (0))l4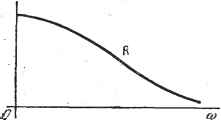

=0(со).

Пример. Чтобы лучше понять механизм перехода от разложения в ряд Фурье к интегралу Фурье, рассмотрим Рис. 2.16. следующий простой пример. Дана

функция времени, состоящая из прямоугольных импульсов высотой h и шириной 2е, повторяющихся с частотой v. Это функция с периодом

Т=\ = (Т>2г). Ее разложение в ряд Фурье будет

Sin тЙ£ ]тШ

Спектр этой функции состоит из счетного числа отдельных линий (соответствующих последовательным целым числам), отстоящих друг от друга на 2Trv.

График функции f (t) и ее спектр для нескольких значений отношения -

приведены на рис. 2.17, где -введено обозначение тО - т. Концы вертикальных линий, изображающих амплитуды, располагаются на кривых

h sin сое

. It о>

показанных на рисунке слева; самый большой максимум на этих кривых равен 2/гме = 2й.

Рассмотрим теперь кривые

h sin СОЕ-

71 о)

показанные на рис. 2.17 справа; самый большой максимум здесь равен

Ординаты правых кривых будут с точностью до коэффициента - равны

относительным амплитудам. Они отличаются от предыдущих множителем й = Дсо, т. е. отнесены к Дш=1. Если Q стремится к нулю, т. е. если импульсы все дальше отстоят друг от друга по времени, сохраняя прежнюю форму, то линии спектра все больше сближаются, левая кривая- величины их амплитуд - все больше сплющивается, но относительные амплитуды на правой кривой остаются неизменными. В пределе, когда Q = О, функция / (t) сводится к одиночному импульсу в начале отсчета времени. Тогда в спектре частот имеется несчетное число линий (т. е. столько, сколько точек на прямой), кривая слева-: бесконечно сплющенная-сливается с осью ш, но

либо ее квадрат (рис. 2.16). Это представление неудобно тем, что не выявляет фаз отдельных составляющих, однако имеет то преимущество, что остается неизменным - при любом перемещении начала отсчета времени t. Действительно, легко заметить, что так же, как в случае спектра для ряда

Фурье, при смещении начала отсчета времени кривая О (со) претерпевает винтообразное скручивание, пропорциональное Iq. Это изменяет составляю-(w)-i-\(w) щие R(co) и 1(со), но не амплитуду