. Tta sin ct . гей sin р (sina sin р \ Eab X I

ад sin а Ttfesinp ~1 I

(sinci sin Р \

откуда диаграммы в плоскостях xOz и yOz будут соответственно описываться формулами

Eab sin и Eab sin к

тса sin а Tzb sin р

Направления нулевого излучения в этих плоскостях получаются из формул

и = /Cit, v = Niz (К, N - целые числа ф 0),

иначе говоря,

sina = -/С, sinS = -z-V а b

или же, поскольку синус приближенно равен дуге, а = -Н, = ~N.

Замечание. В большом количестве случаев раструбы излучающих рупорных антенн прямоугольны, как в рассмотренном примере; кроме того, Е не зависит от координаты, у, а только от координаты х. Тогда диаграмма излучения в плоскости хОу получается из формул (26) и (27) преобразования Фурье с одной переменной ).

ЛИТЕРАТУРА К ГЛАВЕ II

1. Ф и x т е н г о л ь ц Г. М., Курс дифференциального интегрального исчисления т. III, Физматгиз, 1960.

2. С м и р н о в В. 14., Курс высшей математики, т. II. Физматгиз, 1962.

3. Т о л с т о в Г. П., Ряды Фурье, Физматгиз, 1960.

) J. Р. Ramsay, Fourier transforms in aerial theory. The Marconi Review, № 83-88.

заданную диаграмму направленности, то распределение амплитуд в области 5 можно получить с помощью обратного преобразования Фурье.

Пример. Положим, что поле у прямоугольного отверстия излучающей рупорной антенны постоянно. Возьмем точку О в центре прямоугольника и оси Ох и Оу, соответственно параллельные сторонам прямоугольника с длиной а и Ь. Тогда непосредственно получаем

ГЛАВА III ВЕКТОРНОЕ ИСЧИСЛЕНИЕ

3.1. СКАЛЯРНЫЕ ВЕЛИЧИНЫ. ВЕКТОРНЫЕ ВЕЛИЧИНЫ. ОПРЕДЕЛЕНИЯ

Скалярные величины

Величины называются скалярными (скалярами), если они после выбора единицы измерения полностью характеризуются одним числом. Примерами скалярных величин являются угол, поверхность, объем, масса, плотность, электрический заряд, сопротивление, температура.

Следует различать два типа скалярных величин: чистые скаляры и псевдоскаляры.

3.1.1. Чистые скаляры. Чистые скаляры полностью определяются одним числом, не зависящим от выбора осей отсчета. Примером чистых скаляров могут служить температура и масса.

3.1.2. Псевдоскаляры. Как и чистые скаляры, псевдоскаляры определяются с помощью одного числа, абсолютная величина которого не зависит от выбора осей отсчета. Однако знак этого числа зависит от выбора положительных направлений на осях координат *).

Рассмотрим, например, прямоугольный параллелепипед, проекции ребер которого на прямоугольные оси координат соответственно равны а, а, а, Ь, by, b, с. Су, с. Объем этого параллелепипеда определяется с помощью определителя

у

Ьх Ьу

Сх Су

абсолютная величина которого не зависит от выбора прямоугольных осей координат. Однако, если переменить положительное направление на одной из осей координат, то определитель изменит знак. Объем - это псевдоскаляр. Псевдоскалярами являются также угол, площадь, поверхность. Ниже (п. 5.1.8) мы звидим, что псевдоскаляр представляет собой в действительности тензор особого рода.

Векторные величины

3.1.3. Ось. Ось - это бесконечная прямая, на которой выбрано положительное направление. Пусть хх - такая прямая, а направление от л: к л:

*) Иными словами, псевдоскаляры есть величины, которые изменяют знак при переходе от правой системы координат к левой.

Иногда псевдоскалярами называют величины, полностью характеризующиеся одним числом, которое зависит от выбора системы координат (проекция вектора, статический момент и др.), - см., например, [9], стр. 42.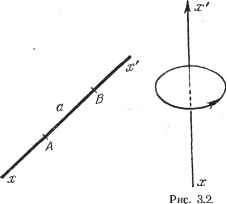

Рис. 3.1.

считается положительным. Рассмотрим отрезок АВ на этой прямой и положим, что число, измеряющее длину АВ, равно а (рис. 3.1). Тогда алгебраическая длина отрезка АВ равна а, алгебраическая длина отрезка ВА равна - а.

Если взять несколько параллельных прямых, то, определив положительное направление на одной из них, мы тем самым определяем его на остальных. Иначе обстоит дело, если прямые не параллельны; тогда нужно специально уславливаться относительно выбора положительного направления для каждой прямой.

3.1.4. Направление вращениЯо Пусть хх - ось. Вращение относительно оси хх назовем положительным или прямым, если оно осуществляется для наблюдателя, стоящего вдоль положительного направления оси, справа и налево (рис. 3.2). В противном случае оно называется отрицательным или обратным.

3.1.5. Прямые и обратные трехгранники. Пусть Oxyz - некоторый трехгранник (прямоугольный или непрямоугольный). Положительные направления выбраны на осях соответственно от О к л:, от О к у и от О к z.

Рассмотрим вращение вокруг оси Oz полуплоскости xOz. приводящее ее к совмещению с полуплоскостью yOz (угол поворота меньше it). Если при этом направление вращения положительно по отношению к оси Oz, то говорят, что трехгранник Oxyz расположен положительно (рис. 3.3, а). В противном случае трехгранник расположен отрицательно (рис. 3.3, б).

При определении расположения трехгранника основное значение имеет порядок следования букв X, у, Z. Действительно, трехгранники Oxyz, Oyzx, Ozxy имеют одно расположение, а трехгранники Oxzy, Oyxz, Ozyx - обратное. Одна перестановка букв х, у, Z меняет расположение трехгранника, две перестановки не меняют.

3.1.6. Векторы. Векторная величина зависит от двух элементов разной природы: алгебраического элемента - числа, измеряющего длину (модуль) вектора, и геометрического элемента -направления вектора. Различают три разных типа векторов. Каждый из них объединяет совокупность векторов с одинаковыми свойствами.

Связанный вектор. Для определения связанного вектора АВ требуется знать: его линию действия {хх), направление на этой линии (от х к х), его начало {А) и неотрицательное число, измеряющее длину а отрезка АВ (рис. 3.4.). Это число а называется модулем вектора.

Если поместить вектор АВ на уже ориентированную ось, то алгебраическая длина этого вектора равна его модулю, взятому со знаком плюс или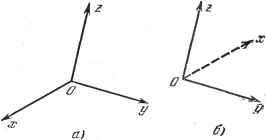

Рис. 3.3.