минус, в зависимости от того, имеют ли вектор и ось одинаковое направление или нет.

Скользящий вектор. Определение остается таким же, как и в предыдущем случае, если исключить требование о закреплении начала вектора. Оно может находиться в любой точке оси хх (рис. 3.5). Силы, рассматриваемые в статической механике, представляют собой скользящие векторы.

Рис. 3.4.

Рис. 3.5.

В самом деле, нельзя нарушить равновесие твердого тела, перемещая точку приложения силы вдоль линии действия этой силы.

Свободный вектор. Такой вектор определяется положительным направлением линии действия и модулем а (рис. З.б). Два одинаково направленных и равных по длине вектора называются эквиполентными. Свободные векторы равны, если они эквиполентны. Обычно свободный вектор обозначают через а.

В начале этой главы мы рассматриваем главным образом свободные векторы, но, когда речь пойдет о векторах поля (п. 3.2.5. и следующие), будут иметься в виду связанные векторы.

Единичный вектор. Это вектор, модуль которого равен единице. Обычно его называют ортом. Орт вектора или оси имеет всегда то же направление, что и рассматриваемый вектор или ось. Единичные векторы координатных осей Ох, Оу, Oz обозначаются соответственно через i, j, k.

Полярный вектор. Осевой вектор. Некоторые векторы не зависят от изменения направления, выбранного на осях координат в качестве положительного (например, сила, скорость, вектор электрического поля). Векторы, обладающие указанным свойством, называются полярными.

Другие векторы, напротив, меняют знак, если изменить направление, выбранное на осях координат в качестве положительного. Такие векторы называются осевыми.

Полярные и осевые векторы существенно отличаются друг от друга по своей природе. Лишь полярные векторы являются векторами в чистом виде. Ниже (п. 5.1.10) мы увидим, что осевой вектор представляет собой антисимметричный тензор второго порядка. В случае трехмерного пространства (только такое пространство и рассматривается нами) число составляющих этого тензора равно 3, поэтому его можно принять за вектор. В четырехмерном пространстве этот особый тензор имел бы б составляющих, тогда как полярный вектор только 4. т. е. там исключена возможность смешения.

Рис. 3.6.

*) Числа Пх, ау, а называются также проекциями (алгебраическими проекциями) и координатами вектора относительно соответствующих осей координат.

Отсюда следует, что векторное равенство может иметь место либо только между полярными векторами, либо только между осевыми. Если, например, вектор, являющийся первым членом векторного равенства,-осевой, той второй член этого равенства тоже должен быть осевым вектором. Такая однородность, присущая векторному исчислению, позволяет обнаруживать вычислительные ощибки.

3.1.7. Положительное расположение трех векторов а, Ь, с. Говорят, что три вектора а, Ь, с расположены положительно (отрицательно), если расположен положительно (отрицательно) трехгранник, имеющий ребра, параллельные этим векторам, таким же образом ориентированные и взятые в том же порядке.

3.1.8. Угол между двумя векторами а и 6. Это угол, не превосходящий тг, на который нужно повернуть вектор а, чтобы совместить его с вектором, эквиполентным Ь, начало которого совпадает с началом вектора а. Он обозначается (а, Ь).

Операции над векторами

3.1.9. Произведение вектора а на скаляр /. Результат умножения вектора а на скаляр / - это вектор с модулем, равным fa, параллельный вектору а, направленный в ту же сторону, что и а, при положительном /ив противоположную при отрицательном /.

В частности, любой вектор а равен произведению его модуля \ а\ - скаляра-на орт и направления вектора а, т. е.

а - \а\и или а = аи. . (1)

3.1.10. Составляющие вектора. Введем три оси прямоугольных координат и рассмотрим геометрические проекции (компоненты) вектора а на эти оси:

а, Оу, а.

Имеем

a = av + aj, + a- . (2)

Используя i - орт оси Ох, можем написать ас = 1а (а - число, измеряющее алгебраическую длину по направлению оси Ох; следовательно, это число положительно, если а и i имеют одинаковое направление, и отрицательно в противном случае). Аналогично

ay = Jay, a = ka.

Таким образом,

a = ia + jay + ka.

Числа ttj, tty, а называются составляющими вектора а относительно соответствующих осей координат *).

3.1.11. Сложение векторов. Сумма нескольких векторов а, Ь, р определяется следующим образом.

Из произвольной точки О проводим вектор OA, эквиполентный вектору а, затем из точки А проводим вектор АВ, эквиполентный вектору Ь, и т. д. до получения точки Р - конца вектора, эквиполентного вектору р (рис. 3.7).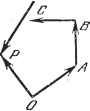

Вектор ОР представляет собой сумму векторов а, Ь, .. ., р. Эта сумма, очевидно не зависит от выбора точки О. Следовательно, вектор суммы s также представляет собой свободный вектор.

Векторное сложение записывается в виде

S==:C + 6+ ... (3)

Из геометрического определения суммы векторов непосредственно следует, что эта операция коммутативна, т. е.

и ассоциативна, т. е.

+ Ф ~{- с) = а ~{- b ~{- с.

Составляющая по оси Ох вектора

суммы S векторов а, b.....р равна

сумме составляющих этих векторов относительно той же оси:

Sx = x + bjc- Л-Рх-

3.1.12. Скалярное произведение. Скалярное произведение двух векторов а tl b - это число, равное прои,эведению трех величин а, b и cos (с, Ь); оно обозначается через с Ь.

Легко заметить, что скалярное произведение коммутативно: а Ь=Ь а и дистрибутивно: {а~\-Ь) с = а с~{-Ь с.

Вопрос об ассоциативности скалярного произведения отпадает, так как формула (а Ь) с не имеет смысла; кроме того, очевидно, неверно равенство (а Ь) с=а(Ь с).

Замечание 1. Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы ортогональны. Действительно, cos (а, Ь) ~ 0;

следовательно, (с, Ь) - .

Замечание 2. Пусть хх-- ориентированная ось, а и - единичный вектор этой оси (рис. 3.8). Тогда скалярное произведение любого вектора с на и равно проекции вектора а на ось хх:

Рис. 3.7.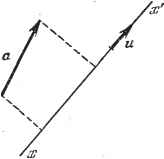

с в = с cos {а, и).

Рис. 3.8.

Замечание 3. Скалярное произведение вектора на самого себя равно квадрату модуля этого вектора:

а а= а.

Замечание 4. Если через i, j, k обозначить единичные векторы осей координат, то

j.k = k- i = i-j = 0, i . ij . j = k- A= 1.

Скалярное произведение в декартовых координатах. Пусть, aj, х Ьу, а. - соответственно проекции на оси Ох, Оу, Oz векторов с и &. Имеем

а - б = {aj -г у/ -1- г*) Фх -1- bj -Г bji).