cos (С, 6) =

3.1.13. Векторное произведение. Векторным произведением двух векторов с, b называют вектор с, длина которого равна c>sin(a, 6) и который перпендикулярен обоим векторам с и б, причем векторы а, Ь и с расположены положительно.

Векторное произведение обозначают так: аХЬ~с.

Замечание. Если ни один из векторов с и б не равен нулю, то выражение аХб==0 означает, что линии действия векторов параллельны, так как sin (с, б) = 0.

Модуль вектора с численно равен площади параллелограмма, построенного на векторах, эквиполентных а и Ь, проведенных через любую точку О пространства.

Это замечание позволяет дать более наглядное определение векторного произведения. Пусть а и b - два вектора. Проведем через точку О векторы

ОЛ и ОВ, эквиполентные с и б (рис. 3.9). Тогда векторное произведение с векторов с и б будет определяться следующим образом.

Модуль вектора с равен числу, измеряющему площадь параллелограмма ОАРВ. Линия действия этого вектора перпендикулярна плоскости ОАВ, а направление его таково, что поворот на угол, не превышающий тг, совмещающий OA с ОВ, происходит в положительном относительно С направлении.

Использование векторного произведения двух векторов OA и ОВ позволяет легко определить алгебраическую площадь треугольника ОАВ. Ориентируем плоскость ОАВ, иначе говоря, выберем в этой плоскости положительное направление вращения. Алгебраическая площадь треугольника ОАВ равна половине алгебраической длины векторного произведения OA X ОВ, отсчитанной вдоль оси, перпендикулярной плоскости ОАВ и ориентированной таким образом, чтобы выбранное направление вращения было для нее положительным (см. п. 3.1.4).

Векторное произведение в декартовых координатах. Так как вектор с = с X б перпендикулярен плоскости АОВ, а модуль его равен площади параллелограмма ОАРВ, то проекция векторного произведения с на Ох равна площади проекции параллелограмма на Oyz. Следовательно,

Cj, = Uyb - aby

По аналогии находим

fy = A - А-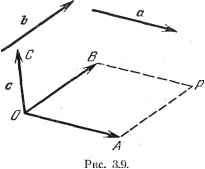

Учитывая дистрибутивность скалярного произведения и замечание 4, получим

с б = аЬ 4- dyby + с А- (5)

Замечание 5. Используя формулу (5) и определение скалярного произведения, получим выражение для косинуса угла между двумя векторами а, b через проекции этих векторов:

o-xbx+a-ybsi + azbz

т. е.

аУ b = i(ab, - aby) + j{abj, - ab,) + k(ab,. - ab. Это выражение можно записать в более симметричной форме:

/ j k

bx by

Перечислим основные свойства векторного произведения.

Эта операция антикоммутативна, т. е. с X б = - b X а. В самом деле, обе тройки векторов с, б, с и Ь, а, с образуют противоположно расположенные трехгранники (см. п. 3.1.5).

Далее, векторное произведение не ассоциативно. Действительно, равенство (с X &) X г = с X (fc X f). вообще говоря, неверно, так как направления векторов, записанных в левой и правой частях этого соотношения, отличаются друг от друга. Однако векторное произведение - операция дистрибутивная, т. е. справедлива формула

(a-hb)X с = аХс+ЬХс.

Эта формула равносильна соотношению

Замечание 1. Векторные произведения ортов координатных осей соответственно равны: ixj=k, jXk=i, kX.i - j.

Замечание 2. Момент вектора а относительно точки О равен векторному произведению rXd- Здесь г - вектор, имеющий начало в точке О. а конец - в любой точке на линии действия вектора а.

3.1.14. Смешанное произведение трех векторов. Смешанным произведением трех векторов называется скаляр

а - (ЬХ с).

Применяя формулы для скалярного и векторного произведений в декартовых координатах, получаем

фХС) = фуС - ЬСу) + ФгСх - Ьхг) у + Фху - byCJ а.

т. е.

а-(ЬХс) =

Мы видим, что смешанное произведение трех векторов численно равно объему параллелепипеда, построенного на трех векторах ОЛ, ОВ. ОС (с общим началом в точке О), эквиполентных векторам а, Ь, с. Объем положителен или отрицателен в зависимости от того, положительно или отрицательно расположены эти три вектора. Следовательно, роль векторов, составляющих смешанное произведение, совершенно одинакова и

фх с) = b (с X а) = с (а X Ь),

а ф Хс) = (а ХЬ) с.

dt dt dt

вектора и т. д.

Если вектор а зависит от нескольких переменных т, 6.....то можно

также определить частные производные а различных порядков.

Если каждому значению переменной t соответствует точка пространства М, то говорят, что точка М есть функция от t. Для наглядности запишем ее в виде Mit). Придадим переменной t приращение Д и рассмотрим вектор

AM = М it + At) -Mit)*).

Если при Д, стремящемся к нулю, модуль этого вектора тоже стремится к нулю, то Mit) есть непрерывная функция от t. Предел вектора

*) Здесь использована запись, введенная Грассманом: вектор АВ обозначается с помощью выражения В - А.

Первая строка показывает, что при круговой перестановке векторов а, Ь, с их смешанное произведение не меняется, вторая - что можно менять местами знаки скалярного и векторного произведений. Последнее обстоятельство служит обоснованием для упрощения обозначения смешанного произведения: оно записывается в виде (сбс) или аЬс.

3.1.15. Двойное векторное произведение трех векторов. Двойное векторное произведение трех векторов выражается формулой

сХ(бХс) = (с-с)б -(с-б)с. (9)

В самом деле, например, проекции на ось Ох векторов левой и правой части этой формулы соответственно равны

ФхСу - Ьус;) - фс - Ьс,).

(йС + СуСу Ч- Jf - ( А + А + Л)

Легко проверить тождественность этих двух выражений.

Используя формулу (9) и правила перестановки векторов, составляющих смешанное произведение, получим

(с X 6) (с Ха)={а c)(b-d) - (a- d)(b с). (10).

(aXb)X{cXit)-=b(acd)--a(bcd). (И)

3.2. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ

Дифференцирование

3.2.1. Производная вектора. Производная точки. Допустим, что каждому значению переменной i соответствует определенный вектор а. В таком случае говорят, что этот вектор является функцией переменной / и записывают его в виде a(t). Дадим переменной t приращение и рассмотрим вектор Аа = а (t-\-At)-а (О- Если при At, стремящемся к нулю, модуль вектора Аа стремится к нулю, то ait) есть непрерывная функция

от t. Предел вектора называется производной вектора ait) по t.

Производная вектора а it) обозначается через или а it). Она равна

da.. day da

h J / Ч~ -;fr Аналогично определяется вторая производная