Используя определение производной первого порядка, можно определить производные точки М высших порядков. Если точка М является функцией нескольких независимых переменных, то для нее определяются также и частные производные.

Замечание. Понятие производной точки сводится к понятию производной вектора. Для этого достаточно зафиксировать любую точку О. Производная точки M(t) представляет собой производную вектора ОМ.

3,2.2. Производная вектора по другому вектору. Даны два вектора а п Ь. Производной вектора а по вектору b называется вектор

который обозначают через

da

Проекции этого вектора на оси Ох, Оу, Oz соответственно равны:

3.2.3. Основные формулы дифференцирования.

Производная суммы. Пусть

s~a-\-b\- ... -(-/ .

Очевидно,

sa + b... -\-р. .

Производная произведения вектора на число. Пусть

b = па.

Очевидно,

Ь = па. - . . .

Следовательно, если п, т.....g - числа, то производная вектора

и=па-\-тЬ-\- ... ~{-gp

равна

и = па + тЬ-{- ... -\-gp. (13)

Производная произведения векторной и скалярной функций. Пусть f{t) и a{t) - скалярная и векторная функции от и и= fa. Тогда

Аи (f--Af)(a + Aa) - fa Аа Af Да А/

А ~~ А ~J At т At .At ,

В пределе получим

u=fafa. (14)

называется производной точки M(t) по t:

dM ,. AM

\а\а - (а-а)а (аХа)Ха fts - -Iftp

Согласно предположению правая часть равенства равна нулю и, значит,

--г- = const. ft

Следовательно, орт направления а постоянен, т. е. направление переменного вектора а неизменно.

3.2.4. Интеграл от вектора. Дан переменный вектор ait):

а it) ~ iuj 4- + ka.

Обозначая через и два значения t, имеем

t, t, (, (,

jait)dt = ij adt + J j adt+k j adt.

функции точки

В математической физике часто рассматривается величина, которая зависит не только от положения точки, т. е. от ее координат х, у, z. но и еще от какой-либо другой переменной, в больщинстве случаев от времени. Если рассматриваемая величина является числом (вектором), то принято говорить, что речь идет о скалярной (векторной) функции точки. В этих случаях говорят также, что в рассматриваемой области пространства задано скалярное или векторное поле.

Например, плотность заряда в различных точках изолированного наэлектризованного тела представляет собой скалярную функцию точки;

Производная скалярного произведения. Пусть a(t) и bit) - две векторные функции и f - ab - их скалярное произведение. Рассмотрим

А/ (а+Да).(Ь4-ДЬ) -а-6 , л , Аа А&

Переходя к пределу, имеем

f = ab + a-b. (15)

Производная векторного произведения. Аналогично предыдущему получим, что производная векторного произведения с = аХЬ равна

c = aXb-{-aXb. (16)

В этой формуле следует внимательно следить за порядком множителей, так как b X а = - а X Ь.

Теорема 1. Пусть а - произвольный переменный вектор. Тогда

II/ а-а

Для вывода этой формулы достаточно продифференцировать тождество а2 = с-с.

Теорема 2. Если переменный вектор с удовлетворяет равенству

а X а ==0, то он параллелен одному и тому же направлению.

а 1а\а - \а\ а Дифференцируя отнощение --г, получаем---,---, но

с = -у-, и, учитывая (9), имеем

электрическое поле, которое создается этими зарядами в различных точках тела, представляет собой векторную функцию точки. Электрические заряды создают скалярное поле плотности и векторное поле электрических сил. Если электрические заряды изменяются в зависимости от времени, то скалярное и векторное поля являются не только функциями координат рассматриваемой точки, но также и функциями времени.

Наиболее важные поля характеризуют следующие три функции:

1) градиент - векторная функция, аргументом которой является скалярная функция точки;

2) дивергенция - скалярная функция, аргументом которой является векторная функция точки;

3) вихрь - векторная функция, аргументом которой является векторная функция точки.

3.2.5. Градиент. Дана скалярная функция /(х, у, z). Градиентом этой функции называется вектор с координатами

дх ду дг

Он обозначается через grad /. Следовательно, согласно определению можно написать

(17)

Пусть Ж(х, у, Z) и M-dM - бесконечно близкие точки поверхности S (рис. 3.10). Скалярное произведение grad / ЙЛ1 равно df. Действительно,

grad / . ЙЛ1 = § + 4 dy + 4~ dz =3 df.

(18)

Отношение j называется производной скалярной функции / в точке М по направлению dM. Формула gtadf-dMdf показывает, что эта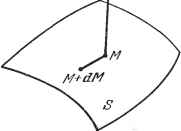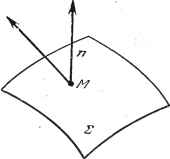

Рис. 3.10.

Рис. 3.11.

производная равна проекции вектора grad / на направление dM, так как

df dM ,

3.2.6, Нормальная производная. Рассмотрим нормаль в точке М к некоторой поверхности £, проходящей через эту точку (рис. 3.11). Производная от / в точке М по направлению нормали называется нормальной производной от / для поверхности Е. Если п-единичный вектор нормали, то эта производная равна grad / ti, т. е. проекции вектора grad / на нормаль п.