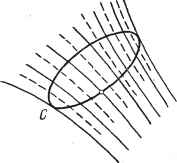3.2.7. Поверхности уровня. Поверхности уровня определяются равенством /(X, у, 2:)== const. Уравнение поверхности уровня, проходящей через точку (Xq, Уо, 2:0), имеет вид

f(x. у, z) = f(Xo, уо, Zo).

Оно геометрически представляет одну поверхность, если функция f(x, у, z) однозначна, что почти всегда и встречается в физике. Вектор grad / в каждой точке нормален к рассматриваемой поверхности уровня, проходящей через эту точку.

Действительно, формула (18) при любом перемещении dM точки М дает grad/ dM-.df. Так как на поверхности уровня / неизменно, то при любом перемещении dM точки М по этой поверхности df = 0. Аналогичное заключение можно сделать в случае, когда точка М перемещается по касательной плоскости, проведенной к поверхности уровня в этой точке. Следовательно, dM и grad / перпендикулярны друг другу. Так как вектор dM - произвольный вектор на касательной плоскости, проведенной в точке М к поверхности уровня, то высказанное утверждение доказано.

3.2.8. Смысл вектора grad/. Вектор grad / полностью описывает поведение функции / в окрестности рассматриваемой точки М. В частности, самое быстрое изменение / происходит при перемещении по нормали к поверхности уровня Это максимальное изменение определяется по величине и направлению вектором grad /.

Для того чтобы представить поле вектора grad/, построим поверхности уровня

/(х, у, z)~kc,

где k~\, 2, а с - достаточно малая постоянная.

Рассмотрим две поверхности уровня 5j и S, соответствующие двум значениям k: п и п~\-1. Пусть УИ -точка поверхности .Sj и d-расстояние от М до S- Вектор grad / будет в точке М нормален к S, направлен

в сторону возрастающих / и по модулю приближенно равен Следова-

у \ тельно, I grad / будет тем больше, чем ближе

друг к другу рассматриваемые поверхности.

Замечание. Как показывает формула grad. f dM~df, вектор grad/ не зависит от выбора осей (см. также п. 3.3.7).

3.2.9. Силовые линии. Кривая, направление которой в каждой точке М совпадает с направлением вектора grad /, соответствующего этой точке, называется силовой линией. Векторное уравнение силовой линии: giad / X dM = 0. Ее скалярные уравнения:

д£

дх ду dz

Рис. 3.12. dx ~~ dy dz -

Следовательно, силовые линии представляют собой ортогональные траектории к поверхностям уровня:

/(х, у, 2)= const. . .

Силовая трубка - это поверхность, описанная силовой линией, перемещающейся вдоль замкнутого контура С (рис. 3.12).

на ось Oz :

Замечание. Дивергенция представима в виде суммы следующих скалярных произведений:

. да . . да . . да

) Иногда вместо rota пишут curia.

3.2.10. Градиент сложной скалярной функции. Если скалярная функция /(т, п, ...) является функцией нескольких скаляров т, которые сами представляют собой функции координат х, у, z, то имеет место формула:

Действительно,

gtauf.dMdf=.dm + dn+ .... .

dm==gTadm dM, dn = grad ti dM.

Отсюда в силу произвольности вектора dM вытекает справедливость формулы (19).

Сравнив эту формулу с формулой для полного дифференциала

d(p = ~ dx~{-- dy~[-- dz. убедимся, что знак grad ведет себя точно

так же, как знак дифференциала.

Применяя формулу (19) к функциям f(m, п) - т-\-п и f {т, п) - тп. получим

grad (m + ) = grad in -(- grad n, grad m/i = m grad -j- grad m. Далее, из соотношения gradf-dM-df следует, что уравнение

grad m=: grad n

равносильно уравнению

m = n-\- const.

3.2.11. Дивергенция и вихрь. Дана векторная функция а точки М(х, у, z). Пусть Uj, Су, - проекции вектора а на соответствующие оси координат.

Дивергенция. Дивергенция вектора а - это скалярная величина

да да да, d- = + -+- (20)

Вихрь. Вихрь вектора а - это векторная величина

/да, да\ 1 да даЛ I да дах\

= + аТ-)-

Следовательно, проекции вектора rot а ) равны:

на ось Ох :

дх ду dz

Применяя его к скаляру /, получаем*)

Скалярное произведение векторов V и с равно:

да dov да

Векторное,произведение векторов V и с равно:

/ да, day, \ I day da, \ I da, day\ Xa-l---) + *(-Wrot . Г25)

Поэтому для функций grad /, div а и rot а часто используются следующие обозначения:

V/, V с, V X

Аналогично получаем

где скалярный оператор у2 == V V обозначен через Д.

*) При выполнении действий по правилам, установленным ранее для обычных

I , d d д

скаляров и векторов, под произведением символов -g. на , скаляр

, , da dtp dv

(X, у, z) будем понимать соответственно скаляры -g, -gj-.

Вихрь представим в виде суммы следующих векторных произведений:

3.2.12. Оператор Лапласа. Оператором Лапласа (лапласианом) называют

дх ду dz Если применить его к скалярной функции, то

~ дх ду dz

Название оператора происходит от уравнения Лапласа, которое записывается в виде Д/ = 0.

Применим оператор Лапласа к вектору а. Имеем

л да I да да дх ду dz

Так как

то для вектора Да получаем следующее выражение:

Дс = i La 4- у Д Су -I- А Д й.

3.2.13. Символический вектор набла (оператор Гамильто:1а). Оператором Гамильтона называют векторный оператор