3.3.3. Теорема Остроградского. Теорема Остроградского - это теорема, выраженная формулой (49): интеграл от дивергенции а, распространенный на объем т, равен потоку вектора а, направленному по внешней нормали через замкнутую поверхность 5, ограничивающую этот объем т **).

*) Используя символический вектор V, можно указать удобное для запоминания операторное соотношение, из которого формулы (48) - (50) получаются в виде частных случаев. Это соотношение имеет вид:

J dtV- j di, da = n da, (*)

где tt - внешняя нормаль к замкнутой поверхности S, ограничиваю-щей объем т. Формула (48) получается в результате умножения обеих частей (*) на скаляр /, (49) в результате скалярного умножения на вектор а и (50) - в результате векторного умножения на вектор а.

**) Формула Остроградского, строго говоря, верна только для пространственно односвязных областей (см. [2J, стр. 336).

3.3.2. Поток вектора. Пусть 5 - двухсторонняя поверхность, М - переменная точка на 6 , а-векторная функция точки М, MN - нормаль к 5, на которой выбрано положительное направление, da - элемент поверхности, окружающий точку М. Обозначим через da вектор, длина которого равна площади da, а направление совпадает с положительным направлением нормали к этому элементу. Потоком вектора а через поверхность 5 называют

двойной интеграл J а da (двойной интеграл берется от скалярного произ-

ведения).

Основные формулы

Пусть 5 - замкнутая поверхность, ограничивающая объем т, М - переменная точка т (или на поверхности S), da - определенный выще вектор, направленный по внешней нормали к поверхности 5. Пусть, далее, / - скалярная и а - векторная функции точки М. Предполагается, что они непрерывны вместе со своими первыми производными в любой точке объема т и его границы 5.

Справедливы следующие три формулы, заменяющие тройной интеграл двойным:

1) формула для градиента

f gtaufd-z j fda; (48)

2) формула для дивергенции (теорема Остроградского)

j (iivadi=z j а - da; (49)

с S

3) формула для вихря *)

JTotadi= jdaXa- (50)

Ддах day дх йу

ду дг

dx dy dz -

. fJdxdydz- fdxdydz+ fdxdydz. J dx J dy дг

T T T

Рассмотрим интеграл j ~dx dy dz и в объеме т с помощью четырех

плоскостей у, y-\-dy, Z, z-\-dz вырежем параллелепипед. На поверхности 5

указанные плоскости вырезают два криволинейных четырехугольника

ABCD и A2B2C2D2, площади которых обозначим через и (рис. 3.15).

л/ .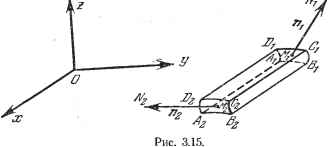

Пусть Ж, и М2 - точки этих четырехугольников, yVIjTVj и MjV, - внешние нормали к поверхности 5, орты которых соответственно щ и ге.

Нормаль yV/jA/i образует с осью Ох тупой угол (i, щ); нормаль M2N2 образует с осью Ох острый угол {i, /tj). Имеем

dydz - - cos (г, j) = cos (f, 2)°2-

Пусть (fljp)i и (fl;j)2 - значения в M- и AIj. Интеграл --dxdydz, распространенный на элемент объема i5iCjDi.425222 равен

./ = УЙ[(0;х)2-(flx)l] = (Jc)2C0S(t, n2)02-b( COs(/. i) i:

COS (i, n = i j, cos {i, - i 2-

Векторы n-da и 2°2 совпадают с векторами и dSj введенными

в предыдущем пункте, если считать, что направление внешней нормали положительно.

Следовательно, имеем

откуда

/ Й (-2 i d42 + (fl Ji i d<v ж,

fdxdydz=faj.da.

Правая часть формулы (49) в декартовых координатах имеет вид л /Л/т Лп Qa, \

а-da

Рассмотрим движение жидкости. Пусть ее плотность р и скорость движения а - соответственно скалярная и векторная функции точки пространства и времени t. Предположим, что 5 - произвольная поверхность в пространстве, заполненном жидкостью, и п - орт внещней нормали к этой поверхности. Масса жидкости, проходящая в направлении п за единицу времени через поверхность 5, равна

j п ра da.

Если поверхность 5 замкнута и ограничивает объем z, то полученная формула дает массу жидкости, вытекающую за единицу времени из z. С другой стороны, увеличение массы жидкости внутри объема z за единицу времени равно

dz.

Применяя теорему Остроградского, получим

j п- pada- I div (pa) dz.

Если предположить, что внутри z отсутствуют источники и стоки, то

/ж~ f dv(pa)dT.

Это равенство справедливо для любого объема z рассматриваемого поля. В силу непрерывности функций и их производных (ср. п. 3.3.7)

- + div(pa)=0. (51)

*) Этот предел представляет собой объемную производную векторного поля.

Тройной интеграл распространяется на объем т, а двойной интеграл на поверхность 5.

Повторяя приведенные рассуждения для j.dxdydz и -j-X

1 -с

X dx dy dz, покажем, что

J uivadz== J {aj-\~ayj~\-ak)-da = j a da.

3.3.4. Смысл скаляра diva. Из формулы Остроградского следует, что полный поток вектора а через замкнутую поверхность, ограничивающую бесконечно малый объем dz, равен div adz. Следовательно, дивергенция, вычисленная в точке векторного поля, приближенно равна потоку, выходящему из единицы объема, окружающего эту точку. Точное значение дивергенции векторного поля а может быть определено следующим образом: