jkn grade-do.

С другой стороны, увеличение количества тепла внутри z равно

ср dx.

Отсюда по аналогии с предыдущим случаем получаем

ср- - div (ft grad 0) = 0.

Это уравнение теплопроводности.

В случае однородной среды и при стационарном распределении темпе-

ратуры (-=о уравнение теплопроводности принимает вид

де =: 0.

3.3.5. Формула для градиента. Положим

а = /6,

где / - скалярная функция точки М, а 6 - произвольный постоянный вектор. Согласно формуле (27)

div а = div(/6) =/div 6-j-6 - grad/. Вектор 6 постоянен, поэтому

div а = Ь grad /. Применим формулу (49) к вектору а:

, 6 J grad fdz = b- f fda.

в силу произвольности вектора 6 отсюда следует формула (48).

3.3.6. Формула для вихря. Пусть b - произвольный постоянный вектор. Тогда по формуле (28) .

- div(a X &) = б rot а, . . .

Уравнение (51) называется уравнением неразрывности жидкости. Если жидкость несжимаемая, то

div (pa) = 0.

Если, кроме того, скорость а равна производной от скалярного потенциала V, а плотность р постоянна, то уравнение неразрывности принимает вид

ДУ = 0.

Это уравнение можно непосредственно применить к электрическому полю, если вместо плотности жидкости р взять плотность электрических зарядов движущихся со скоростью а.

Введем обозначения: 6 - температура, р-плотность, k - коэффициент внутренней теплопроводности и с - удельная теплоемкость тела в рассматриваемой точке (скалярные функции). Количество тепла, вытекающего через поверхность 5, равно

6 j rotadz - b J daXa.

В силу произвольности вектора 6 отсюда следует справедливость формулы (50).

3.3.7. Инвариантность*) градиента, дивергенции, вихря. Докажем инвариантность дивергенции. Имеем (формула (49))

J div adz= j а - da.

Введем новые оси координат, и пусть divja - дивергенция, полученная в новой системе координат. Так как скалярное произведение а da не зависит от выбора системы координат, то для любого объема z имеет место равенство

J div adz= j divj a dz

J(divia - diva)dz = Q. (*)

Если в какой-либо точке divjC отличается от dive, то эту точку можно окружить объемом, внутри которого divjo: - diva была бы не равна нулю и сохраняла знак (вследствие непрерывности частных производных вектора а). Следовательно, для этого объема интеграл

J (divi а - div а) dz

был бы не равен нулю, что противоречит (*). Поэтому для любых осей координат divja = diva, т. е. скаляр diva инвариантен относительно выбора координатной системы.

Пользуясь формулами (48) и (50), можно провести аналогичное доказательство инвариантности векторов grad/ и rota относительно выбора осей координат.

3.3.8. Формула Грина. Пусть 5 - замкнутая поверхность, ограничивающая объем z, р к д - две скалярные функции точки М. Докажем, что имеет место формула Грина:

J(pAq~qAp)dz= j{pgtadg - qgTadp) da. Используя формулу (27), получаем

div (p grad q) = p div grad q -\- grad q grad p~ pAq-\- grad q grad p.

*) Независимость от выбора координатной системы.

так как rot 6=== 0. Подставим в формулу (49) вместо вектора а вектор ауЬ:

Ь j TOtadz= j{aXb) da.

Смешанное произведение (aX b) da = Ь (da X а) (см. п. 3.1.14),

следовательно.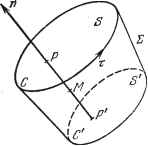

*) Тем самым определяется рассматриваемая сторона поверхности. Очевидно что выбор стороны поверхности и ее ориентация взаимно определяют друг друга.

**) В самом деле, пусть M-\-dM соответствует точка 7И а P-\-dP - точка Р,. Тогда dMMMi,dP = PPi. Имеем ДЖР=Ж,Р, - МР= М,М +МР+РР, -МР = = dP - dM. С другой стороны, К МР к d МР = d (In) = Idn + ndl, т. е. dP - dM = = Idn-{-ndl.

Подставим в формулу (49) вместо вектора а вектор /7 grad 9. Имеем j {рАд-\- grad р grad q)dz- j р grad q da.

Меняя роли функций p к q, находим

j (q Арgrad q grad p) dz = j qgrad p da.

Вычитая последнее выражение из предыдущего, получим формулу Грина.

3.3.9. Формула Стокса. Пусть двухсторонняя поверхность 5 ограничена замкнутой кривой С, на которой указано определенное направление обхода. Нормали к поверхности 5 ориентируем таким образом, чтобы выбранное на С направление обхода оказалось положительным *).

В каждой точке Р поверхности 5 отложим вдоль отрицательного направления нормали отрезки постоянной длины РР. Точки Р, соответствующие точкам Р, образуют поверхность параллельную поверхности 5 и ограниченную замкнутой кривой С. Обозначим через Е поверхность, образованную нормалями, соединяющими точки кривых С и С. Пусть z - объем тела, ограниченного поверхностями 5, S, Е (рис. 3.16).

Будем считать, что отложенная вдоль направления нормали постоянная длина достаточно мала. Рис. 3.16. Пусть, Л1-точка внутри или на поверхности рассматриваемого тела z. Опустим из точки М перпендикуляр MP к поверхности 5; I - длина MP. Тогда MP = In, гае. п - единичный вектор нормали.

Рассмотрим точку M-\-dM (см. п. 3.2.1). Ей соответствует точка P-\-dP. Имеем

dP - dM = ldn-ndl**).

Это выражение умножим скалярно на га:

п- dP - га dM = In dn-{-n п dl.

Но n-dP=Q, так как векторы га и dP перпендикулярны. Кроме того, n-dn=0, потому что вектор постоянной длины перпендикулярен своей производной (это следует из теоремы 1 п. 3.2.3). Учитывая также, что га га=1, получаем

- n-dM = dl.

Далее, согласно (18) grad l-dM = dl. Следовательно, при любом dM имеет место -га dM -grad I dM. Поэтому п - - grad I. Возьмем вихрь от обеих частей этого равенства. Имеем

rot га = -. rot grad / = 0. ,